Previous
|
About HAPcryst: Three-dimensional
flat manifolds
described as quotients of polytopes
|
next
|
|
A
euclidean crystallographic group
G is, by definition, a group of affine transformations of n-dimensional
euclidean space whose subgroup of translations is free abelian of rank
n. One says that G is Bieberbach
if each non-trivial transformation has no fixed point. If G is
Bieberbach then the quotient M=Rn/G is a flat manifold.
Tha GAP package Cryst contains the list of 219 three-dimensional space
groups. The following commands from the ACLIB package show that 10 of
these are Bieberbach. |
gap>
3dBieberbach:=[];
gap> for n in [1..219] do
gap> if IsAlmostBieberbachGroup(Range(IsomorphismPcpGroup(
SpaceGroup(3,n) ))) then
gap> Add(3dBieberbach,n);
gap> od;
gap> 3dBieberbach;
[ 1, 4, 7, 9, 19, 33, 34, 76, 142, 165 ]
|
A
convex polytopal fundamental domain for the action of a Bieberbach
group can be computed using the HAPcryst package (written by Marc
Röder)
and Polymake software. For the 3-dimensional case these fundamental
domains can be visualized using Javaview. The corresponding flat
manifold is obtained by appropriately identifying facets of the
fundamental domain: identified faces are given identical colours.
For example, the Bieberbach group G=SpaceGroup(3,9) admits a
permutaheral fundamental domain:
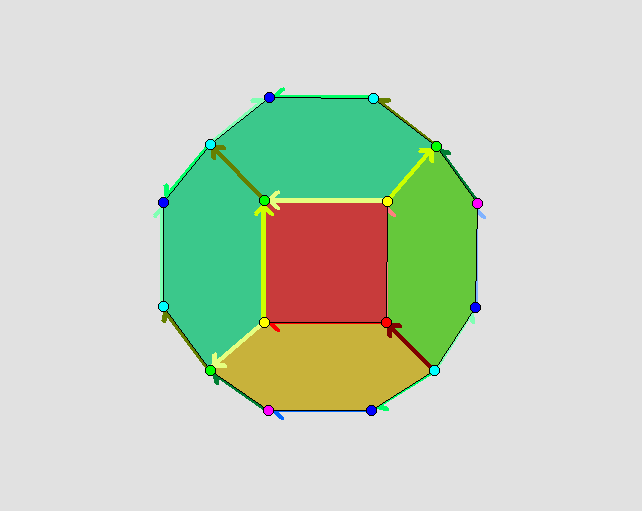
Of course, a given Bieberbach
group can admit several combinatorially different convex fundamental
domains.
|
Javaview
images (which can be rotated etc.) of fundamental domains and
tesselations for the 10
three-dimensional Bieberbach groups have been produced by Marc
Röder and can be viewed here.
(If you don't have Javaview installed then an html example is
given here.)
|
|
