| Previous |
About HAP: Cohomology of some Artin groups |
next |
A Coxeter diagram is a finite graph D with at most one edge joining any pair of vertices, and with each edge labelled by an integer n>2 or n=infinity. The label n=3 occurs frequently and so, in pictures of D, we denote it by an unmarked edge. For typographical reasons, when the label is infinity we shall denote it by the symbol 0 (but treat it as infinity in any mathematical discussion). Here are three examples.
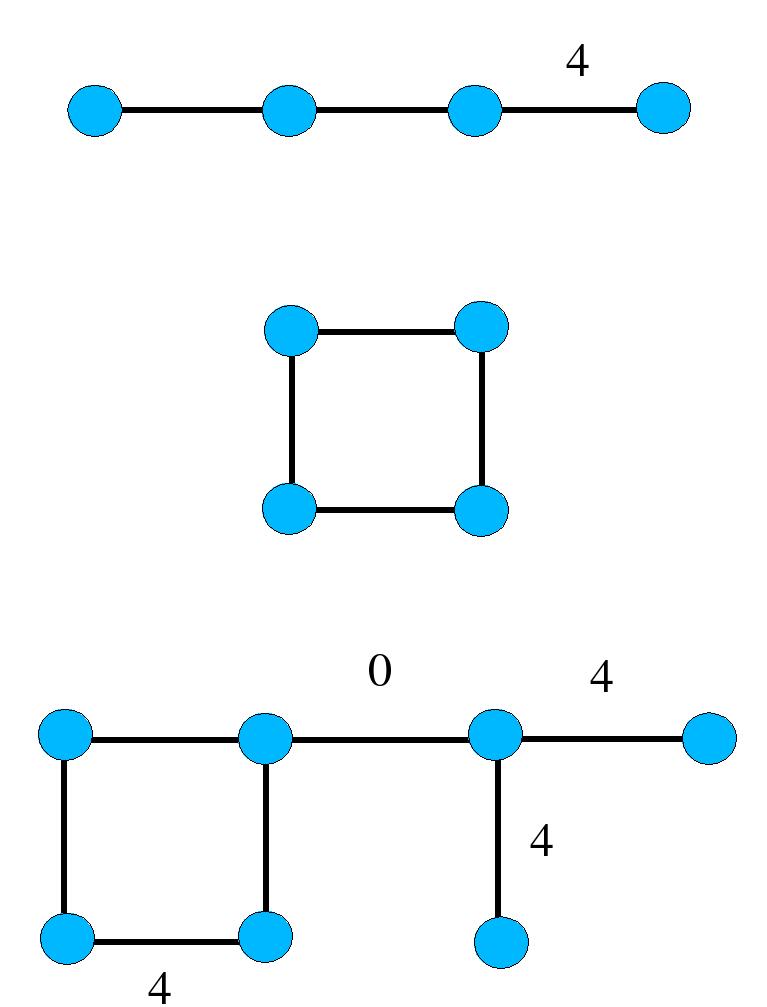
We can succinctly represent a Coxeter graph by numbering its vertices and recording a list D = [L1, ... Lt] in which each term is itself a list Lk = [vk, [uk1,nk1], [uk2,nk2], ... [ukm,nkm]] such that vertex vk is connected to vertex ukj by an edge with label nkj. It is sufficient to record just those vertices ukj > vk. We set nkj=0 when the edge label is infinity.
The above three diagrams are encoded by the following commands.
gap> D2:=[ [1,[2,3],[4,3]], [2,[3,3]], [3,[4,3]] ];;
gap> D3:=[ [1,[2,3],[4,3]], [2,[3,3],[5,0]], [3,[4,4]], [5,[6,4],[7,4]] ];;
- There is one generator x for each vertex in D.
- There is one relator (xy)n = (yx)n for each pair of vertices not connected by an infinity edge in D where: if the vertices x,y are connected by no edge then n=2, otherwise n is the edge label; the word (xy)n = xyxyx... is a product of precisely n generators.
The following commands give the Artin group associated the first of the above diagrams, and the Coxeter group associated to the second.
[ <free group on the generators [ f1, f2, f3, f4 ]>,
[ f1*f2*f1*f2^-1*f1^-1*f2^-1, f1*f3*f1^-1*f3^-1, f1*f4*f1^-1*f4^-1,
f2*f3*f2*f3^-1*f2^-1*f3^-1, f2*f4*f2^-1*f4^-1,
f3*f4*f3*f4^-1*f3^-1*f4^-1 ] ]
gap> CoxeterDiagramFpCoxeterGroup(D2);
[ <free group on the generators [ f1, f2, f3, f4 ]>,
[ f1*f2*f1*f2^-1*f1^-1*f2^-1, f1*f3*f1^-1*f3^-1,
f1*f4*f1*f4^-1*f1^-1*f4^-1, f2*f3*f2*f3^-1*f2^-1*f3^-1,
f2*f4*f2^-1*f4^-1, f3*f4*f3*f4^-1*f3^-1*f4^-1, f1^2, f2^2, f3^2, f4^2 ] ]
true
gap> CoxeterDiagramIsSpherical(D2);
false
gap> CoxeterDiagramIsSpherical(D3);
false
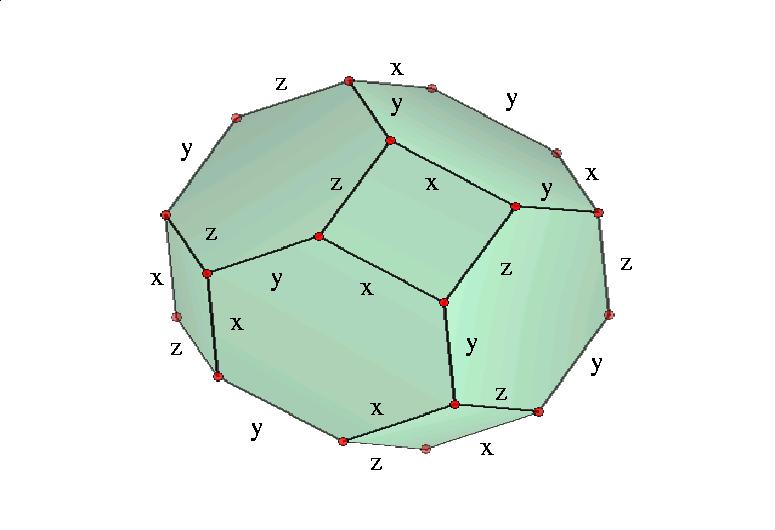
The resolution for a spherical Artin group AD can be obtained as the cellular chain complex of an easily constructed cellular space XD. For the construction we note that the finite Coxeter group WD is isomorphic to a group generated by d reflections in Euclidean space Rd, where d is the number of vertices in the diagram D. Choose any vector v in Rd which is fixed by no reflection in WD. The convex hull of the orbit of v under the action of WD is then a polytope whose 1-skeleton can be viewed as the cayley graph of WD. The edges of faces in the polytope are thus labelled by the generating reflections in WD. Let YD be the space obtained from this polytope by identifying all similary labelled faces (in all dimensions <d). The space XD is the universal cover of YD.
As an example, the space YD for the 3-generator braid group is obtained by identifying similarly labelled faces of the following 3-dimensional polytope.
gap> TR:=TensorWithIntegers(R);;
gap> Homology(TR,1);
[ 0, 0 ]
gap> Homology(TR,2);
[ 2, 0, 0 ]
gap> Homology(TR,3);
[ 0, 0 ]
gap> TRHomology(R,4);
[ 0 ]
For example, any Artin group AD has a normal subgroup 2AD , the even subgroup, consisting of all products of an even number of generators of AD. The following commands show that the even subgroup of the 5-string braid group has integral homology H1(2AD,Z)=Z, H2(2AD,Z)=Z2+Z2, H3(2AD,Z)=Z5, Hn(2AD,Z)=0 for n>3.
(As a curiosity, we note that similar commands can be used to show that, for certain Coxeter diagrams such as D=E7, the Artin group has the same integral homology as its even subgroup.)
gap> R:=ResolutionArtinGroup(D,5);;
gap> A_D:=R!.group;;
gap> 2A_D:=EvenSubgroup(A_D);;
gap> S:=ResolutionSubgroup(R,2A_D);;
gap> TS:=TensorWithIntegers(S);;
gap> for i in [1..4] do
> Print(Homology(TS,i),"\n");
> od;
[ 0 ]
[ 2, 2 ]
[ 5 ]
[ ]
The conjecture has been studied by many people. It is discussed in [G. Ellis & E. Sköldberg,"The K(pi,1) conjecture for a class of Artin groups. Comment. Math. Helv., 85, no. 2, 409--415 (2010)]. That preprint gives a short proof of the following result.
| Suppose that XT is contractible for every connected
full subgraph T of D where T involves no infinity edges. Then XD is contractible. |
(A special case of the above result, in which each AT is assumed to be spherical, was proved in [R. Charney and M.W. Davis, "The K(\pi,1) problem for hyperplane complements associated to infinite reflection groups", Journal Amer. Math. Soc., vol. 8, issue 3 (1995), 597-627].)
The paper explains how a lemma in [ K.J. Appel and P.E. Schupp, "Artin groups and infinite Coxeter groups", Invent. Math., 72 (1983), 201-220] implies the following result.
| Let x, y, z be an arbitrary triple
of vertices in D. Let nxy denote the label on the edge
joining x and y when such an edge exists; otherwise let nxy=2.
The space XD is contractible if 1/nxy + 1/nyz +
1/nxz < 1 or = 1.
|
| The space XD is contractible
when the diagram D is an n-sided polygon with each side labelled
by n=3. (The corresponding group AD is called the affine braid group.) |
The following commands completely determine the additive structure of the integral homology of the affine braid groups on six, seven, eight and nine generators.
gap> R:=ResolutionArtinGroup(D6gens,7);;
gap> TR:=TensorWithIntegers(R);;
gap> for n in [1..6] do
> Print(Homology(TR,n),"\n");
> od;
[ 0 ]
[ 2, 0 ]
[ 2, 2, 0 ]
[ 3, 3, 3, 3, 0 ]
[ 0, 0 ]
[ ]
gap> D7gens:=[ [1,[2,3],[7,3]], [2,[3,3]], [3,[4,3]], [4,[5,3]], [5,[6,3]], [6,[7,3]] ];;
gap> R:=ResolutionArtinGroup(D7gens,8);;
gap> TR:=TensorWithIntegers(R);;
gap> for n in [1..7] do
> Print(Homology(TR,n),"\n");
> od;
[ 0 ]
[ 2, 0 ]
[ 2, 0 ]
[ 6, 0 ]
[ 0 ]
[ 0 ]
[ ]
gap> D8gens:=[ [1,[2,3],[8,3]], [2,[3,3]], [3,[4,3]], [4,[5,3]], [5,[6,3]], [6,[7,3]], [7,[8,3]] ];;
gap> R:=ResolutionArtinGroup(D8gens,9);;
gap> TR:=TensorWithIntegers(R);;
gap> for n in [1..8] do
> Print(Homology(TR,n),"\n");
> od;
[ 0 ]
[ 2, 0 ]
[ 2, 0 ]
[ 2, 2, 6, 0 ]
[ 3, 3, 0 ]
[ 2, 2, 2, 2, 4, 4, 0 ]
[ 0, 0 ]
[ ]
gap> D9gens:=[ [1,[2,3],[9,3]], [2,[3,3]], [3,[4,3]], [4,[5,3]], [5,[6,3]], [6,[7,3]], [7,[8,3]], [8,[9,3]] ];;
gap> R:=ResolutionArtinGroup(D9gens,10);;
gap> TR:=TensorWithIntegers(R);;
gap> for n in [1..9] do
> Print(Homology(TR,n),"\n");
> od;
[ 0 ]
[ 2, 0 ]
[ 2, 0 ]
[ 2, 6, 0 ]
[ 6, 0 ]
[ 2, 6, 0 ]
[ 0 ]
[ 0 ]
[ ]
| Previous
Page |
Contents |
Next
page |