| Previous |
About HAP: Explicit cocycles |
next |
f : G × G × ...
× G → A
satisfying a certain algebraic
cocycle
condition.
Bearing in mind that a standard n-cocycle really just assigns an element f(g1, ... ,gn) of A to an n-simplex in the nerve of G, the cocycle condition is a very natural one which states that "f must vanish on the boundary of a certain (n+1)-simplex". For n=2 the condition is that a 2-cocycle f(g1,g2) must satisfy g.f(h,k) + f(g,hk) = f(gh,k) + f(g,h) for all g,h,k in G. This equation is explained by the following picture.
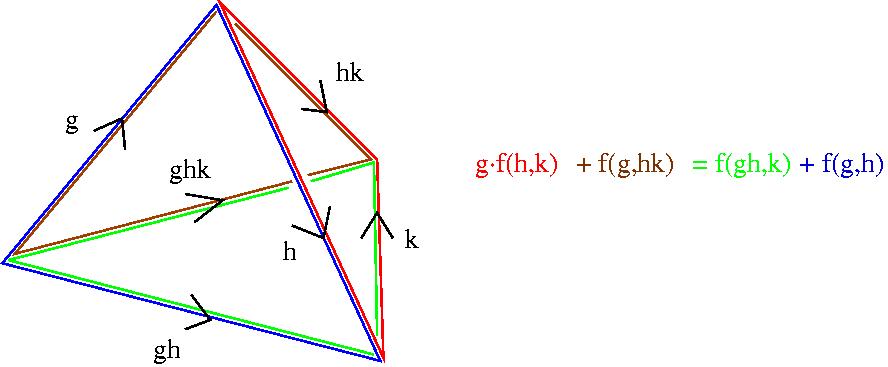
The definition of a cocycle clearly depends on the choice of ZG-resolution R. However, the cohomology group Hn(G,A), which is a group of equivalence classes of n-cocycles, is independent of the choice of R.
There are some occasions when one needs explicit examples of standard cocycles. For instance:
Bearing in mind that a standard n-cocycle really just assigns an element f(g1, ... ,gn) of A to an n-simplex in the nerve of G, the cocycle condition is a very natural one which states that "f must vanish on the boundary of a certain (n+1)-simplex". For n=2 the condition is that a 2-cocycle f(g1,g2) must satisfy g.f(h,k) + f(g,hk) = f(gh,k) + f(g,h) for all g,h,k in G. This equation is explained by the following picture.

The definition of a cocycle clearly depends on the choice of ZG-resolution R. However, the cohomology group Hn(G,A), which is a group of equivalence classes of n-cocycles, is independent of the choice of R.
There are some occasions when one needs explicit examples of standard cocycles. For instance:
- Let G be a finite group and K a field of characteristic 0. The group algebra K(G) and the algebra F(G) of functions đg:G→K, h→đg,h are both Hopf algebras. The tensor product F(G) (×) K(G) also admits a Hopf algebra structure known as the quantum double D(G). A twisted quantum double Df(G) was introduced in [R. Dijkraaf, V. Pasquier & P. Roche, "Quasi-Hopf algebras, group cohomology and orbifold models", Nuclear Phys. B Proc. Suppl. 18B (1991) 60-72]. The twisted double is a quasi-Hopf algebra depending on a 3-cocycle f:G×G×G→K. The multiplication is given by (đg (×) x)(đh (×) x) = đgx,xhßg(x,y)(đg (×) xy) where ßa is defined by ßa(h,g) = f(a,h,g) f(h,h-1ah,g)-1 f(h,g,(hg)-1ahg) . Although the algebraic structure of Df(G) depends very much on the particular 3-cocycle f, representation theoretic properties of Df(G) depend only on the cohomology class of f.
- An explicit 2-cocycle f:G×G→A is needed to construct the multiplication (a,g)(a',g') = (a + g·a' + f(g,g'), gg') in the extension a group G by a ZG-module A determined by the cohomology class of f in H2(G,A).
- In work on coding theory and Hadamard matrices a number of papers have investigated square matrices (aij) whose entries aij=f(gi,gj) are the values of a 2-cocycle f:G×G → Z2 where G is a finite group acting trivially on Z2. See for instance [K.J. Horadam, "An introduction to cocyclic generalised Hadamard matrices", Discrete Applied Math, 102 (2000) 115-130].
We first compute a ZG-resolution R. The Universal Coefficient Theorem gives an isomorphism H3(G,U(1)) = HomZ(H3(G,Z), U(1)), The multiplicative group U(1) can thus be viewed as Zm where m is a multiple of the exponent of H3(G,Z).
gap> R:=ResolutionFiniteGroup(G,4);;
gap> TR:=TensorWithIntegers(R);;
gap> Homology(TR,3);
[ 6 ]
gap> R.dimension(3);
4
gap> R.dimension(4);
5
Mf = 0 modulo 6
where the matrix M is got from the following command.
[ [ 0, 0, 0, 0 ], [ 0, 0, 1, 1 ], [ 1, 1, 0, 0 ], [ 1, 1, 1, 1 ] ]
gap> SolutionsMod3:=NullspaceModQ(TransposedMat(M),3);
[ [ 0, 0, 0, 0 ], [ 0, 0, 0, 1 ], [ 0, 0, 0, 2 ], [ 0, 0, 1, 0 ],
[ 0, 0, 1, 1 ], [ 0, 0, 1, 2 ], [ 0, 0, 2, 0 ], [ 0, 0, 2, 1 ],
[ 0, 0, 2, 2 ] ]
[ 3, 3, -1, -1 ]
gap> Standard_f:=StandardCocycle(R,f,3,6);;
gap> g:=Random(G); h:=Random(G); k:=Random(G);
(1,2)
(1,3,2)
(1,3)
gap> Standard_f(g,h,k);
3
g·f(h,k,l) -
f(gh,k,l) + f(g,hk,l) - f(g,h,kl) + f(g,h,k) = 0
for all g,h,k,l in G. In the above
example the group G=S3
acts trivially on A=Z6. The following commands show that the
standard 3-cocycle produced in the example really does satisfy this
3-cocycle condition.
gap> Test:=function(g,h,k,l);
> return sf(h,k,l) - sf(g*h,k,l) + sf(g,h*k,l) - sf(g,h,k*l) + sf(g,h,k);
> end;
function( g, h, k, l ) ... end
gap> for g in G do for h in G do for k in G do for l in G do
> Print(Test(g,h,k,l),",");
> od;od;od;od;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,6,6,0,0,6,
0,0,0,0,0,6,6,6,0,6,0,12,12,6,12,6,0,12,6,0,6,6,0,0,0,0,0,0,0,12,12,6,6,6,0,
6,6,0,6,6,0,0,-6,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,0,0,0,0,0,0,6,0,0,6,6,0,6,6,
0,6,0,0,6,6,6,0,0,0,0,0,0,0,-6,0,0,-6,0,-6,0,0,0,0,0,0,0,0,6,6,0,6,0,0,6,0,0,
0,0,0,6,6,6,0,0,0,6,6,6,0,0,0,0,-6,0,6,6,0,0,0,0,0,0,0,12,6,6,0,6,0,0,0,0,12,
6,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,0,0,6,0,0,0,0,0,6,6,
6,0,0,0,6,12,6,6,0,0,0,-6,0,0,6,0,0,0,0,0,0,0,12,12,6,6,6,0,0,0,0,6,6,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,0,6,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,
6,6,0,6,6,0,12,12,6,12,12,0,0,0,0,0,0,0,6,6,0,0,0,0,6,6,6,12,12,0,-6,-6,0,0,
0,0,6,6,0,0,6,0,0,6,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,
0,6,0,0,6,0,0,0,0,0,0,0,0,0,0,0,6,6,0,6,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,6,0,6,6,0,6,0,0,6,6,6,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,-6,0,6,0,6,0,6,0,0,0,0,0,0,0,12,12,6,12,12,0,6,6,0,6,6,0,
0,0,0,0,0,0,12,12,6,12,12,0,6,6,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,
0,0,0,0,0,0,6,0,0,6,6,0,6,6,0,6,0,0,6,6,6,0,0,0,-6,0,0,0,-6,0,0,-6,0,-6,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,6,6,0,0,0,0,0,0,0,6,6,0,0,0,
0,0,0,0,6,6,0,-6,0,0,-6,0,0,12,6,0,-6,-6,0,0,0,0,6,6,0,0,6,0,0,6,0,6,6,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,-6,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,6,12,0,6,0,0,6,0,0,0,6,0,0,0,0,0,0,
0,6,12,0,0,0,0,0,0,0,6,6,0,-6,-6,0,0,0,0,0,0,0,0,6,0,0,6,0,6,6,0,0,0,0,0,0,0,
6,0,0,0,6,0,0,6,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,
0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,6,6,0,6,6,0,6,6,6,12,12,0,0,0,0,0,0,0,6,6,0,
6,6,0,6,6,6,12,12,0,0,0,0,0,0,0,6,6,0,0,6,0,0,6,0,6,6,
| Previous
Page |
Contents |
Next
page |