Previous
 About HAP: Simplicial, Cubical, Permutahedral and Regular CW-Complexes
 next

1. Simplicial Complexes
A finite simplicial complex can be created in HAP by specifying its maximal simplices. For instance, the following commmands construct the simplicial projective plane



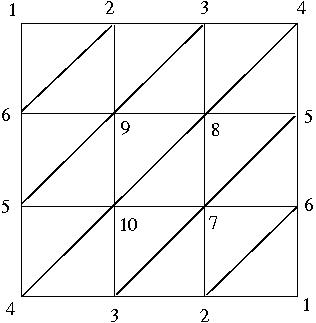
and then calculate its integral homologies from the associated cellular chain complex.
gap> L:=[[1,2,6],[2,6,9],[2,3,9],[3,8,9],[3,4,8],[4,5,8],
> [5,6,9],[5,9,10],[8,9,10],[7,8,10],[5,7,8],[5,6,7],
> [4,5,10],[3,4,10],[3,7,10],[2,3,7],[2,6,7],[1,2,6]];;

gap> P:=MaximalSimplicesToSimplicialComplex(L);
Simplicial complex of dimension 2.

gap> C:=ChainComplex(P);
Chain complex of length 2 in characteristic 0 .

gap> Homology(C,0);
[ 0 ]
gap> Homology(C,1);
[ 2 ]
gap> Homology(C,2);
[  ]
The following commands compute the low-dimensional integral homologies of a 10-dimensional simplicial sphere.
gap> n:=10;;
gap> S:=MaximalSimplicesToSimplicialComplex(Combinations([0..n+1],n+1));
Simplicial complex of dimension 10.

gap> C:=ChainComplex(S);
Chain complex of length 10 in characteristic 0 .

gap> List([0..n],m->Homology(C,m));
[ [ 0 ], [  ], [  ], [  ], [  ], [  ], [  ], [  ], [  ], [  ], [ 0 ], [  ] ]
The simplicial complex arising as the order complex of the poset of non-trivial elementary abelian p-subgroups of a finite group G has been studied by D. Quillen and others. The following commands contruct this simplicial complex for the Sylow 2-subgroup of the Mathieu group M12 (with p=2), and then verify that in this case the simplicial complex is contractible.
gap> Q:=QuillenComplex(SylowSubgroup(MathieuGroup(12),2),2);
Simplicial complex of dimension 2.

gap> C:=ChainComplex(Q);
Chain complex of length 2 in characteristic 0 .

gap> Homology(C,0);
[ 0 ]
gap> Homology(C,1);
[  ]
gap> Homology(C,2);
[  ]
2. Pure Cubical Complexes
In HAP we us the term pure cubical complex to mean a subspace of d-dimensional Euclidian space arising as a union of finitely many d-dimensional unit cubes whose vertices have integral coordinates. A pure cubical complex can be created by specifying a d-dimensional array of 0s and 1s. For instance, the following commands construct a 3-dimensional cubical 2-sphere and determine its homology in low dimensions.
gap> a:=[[1,1,1],[1,1,1],[1,1,1]];;
gap> b:=[[1,1,1],[1,0,1],[1,1,1]];;
gap> c:=[[1,1,1],[1,1,1],[1,1,1]];;
gap> array:=[a,b,c];;
gap> S2:=PureCubicalComplex(array);
Pure cubical complex of dimension 3.

gap> C:=ChainComplex(S2);
Chain complex of length 3 in characteristic 0 .

gap> Homology(C,0);
[ 0 ]
gap> Homology(C,1);
[  ]
gap> Homology(C,2);
[ 0 ]
gap> Homology(C,3);
[  ]
There is a functor

N: (Pure Cubical Complexes)  ------>  (Simplicial Complexes)

that sends a pure cubical complex X to a simplicial complex NX of the same homotopy type. If X is d-dimensional then we refer to the d-dimensional cells in X as facets. The vertices of NX are the facets of X, and the dimensional simplices of NX are the subsets of this vertex set having a non-trivial common intersection. We refer to NX  as the Cech complex of X. The following commands compute the Cech complex of the above cubical 2-sphere and (again) determine the low dimensional homology of the 2-sphere.
gap> NS2:=CechComplexOfPureCubicalComplex(S2);
Simplicial complex of dimension 3.

gap> C:=ChainComplex(NS2);
Chain complex of length 3 in characteristic 0 .

gap> Homology(C,0);
[ 0 ]
gap> Homology(C,1);
[  ]
gap> Homology(C,2);
[ 0 ]
gap> Homology(C,3);
[  ]
The above cubical 2-sphere S2 has twenty-six 3-cells. The following commands compute a homotopy retract with just six 3-cells.
gap> R:=ContractedComplex(S2);
Pure cubical complex of dimension 3.

gap> C:=ChainComplex(S2);;
gap> D:=ChainComplex(R);;
gap> C!.dimension(3);
26
gap> D!.dimension(3);
6
The two-sphere S2 and its homotopy retract R can be visualized using the following commands. These commands invoke the Asymptote vector graphics package.
gap> ViewPureCubicalComplex(S2);
gap> ViewPureCubicalComplex(R);

  

The following command shows that the Cech complex of this smaller 3-dimensional 2-sphere is actually a 2-dimensional simplicial complex.
gap> S:=CechComplexOfPureCubicalComplex(R);
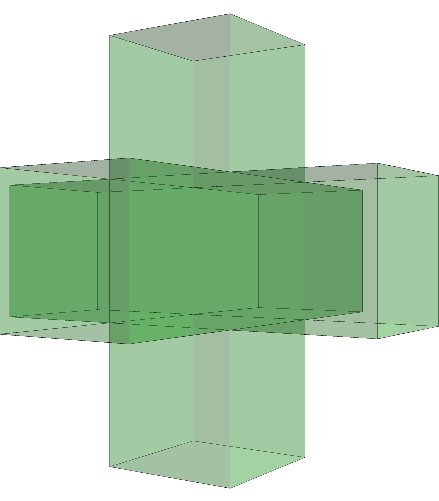
Simplicial complex of dimension 2.
A digital photograph can be represented as a 2-dimensional pure cubical complex. This is done by choosing an integer threshold and including a 2-cell in the pure cubical complex for each pixel where the sum of the three RGB values iis less than the threshold.

The following commands use a threshold of 400 to represent the image



as a pure cubical complex. The complex has 40949 2-dimensional cells.
gap> image:=ReadImageAsPureCubicalComplex("bw_image.bmp",400);
Pure cubical complex of dimension 2.

gap> C:=ChainComplex(image);
Chain complex of length 2 in characteristic 0 .

gap> C!.dimension(0);
45664
gap> C!.dimension(1);
86630
gap> C!.dimension(2);
40949
The number of cells in the above cubical complex makes it difficult to compute the homology of the associated cellular chain complex. One way around the difficulty is to:
  1. Find a homotopy retract R of the pure cubical complex.
  2. Find a large contractible  subcomplex  S in R.
  3. Construct the quotient  C(R)/C(S) of the cellular chain complexes.
  4. Use the fact that Hn(R) =  Hn( C(R)/C(S) ) for n>0 and that H0(R) is isomorphic to the direct sum H0(C(R)/C(S))+H0(S).
The following commands apply Steps 1-4 in order to calculate that the above image has 3 path components and 20 1-cycles.
gap> image:=ReadImageAsPureCubicalComplex("bw_image.bmp",400);
Pure cubical complex of dimension 2.

gap> R:=ContractedComplex(image);
Pure cubical complex of dimension 2.

gap> S:=ContractibleSubcomplexOfPureCubicalComplex(R);
Pure cubical complex of dimension 2.

gap> C:=ChainComplexOfPair(R,S);
Chain complex of length 2 in characteristic 0 .

gap> Homology(C,0);
[ 0, 0 ]

gap> Homology(C,1);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
3. Cubical Complexes
We us the term cubcial complex to mean any cellular subcomplex of a pure cubcial complex. This slightly more general notion allows us to work with smaller homotopy retracts when making homology computations.

The following commands produce a pure cubical homotopy retract R, and then a cubcial retract K, of the above black and white image. Considered as CW-complexes, R involves a total of 16975 cells while K involves a total of 7005 cells
gap> image:=ReadImageAsPureCubicalComplex("bw_image.bmp",400);
Pure cubical complex of dimension 2.

gap> R:=ContractedComplex(image);
Pure cubical complex of dimension 2.

gap> K:=PureCubicalComplexToCubicalComplex(R);
Cubical complex of dimension 2.

gap> Size(K);
16975

gap> ContractCubicalComplex(K);

gap> Size(K);
7005
By working with arbitrary (non-regular) CW-complexes we can further reduce the number of cells in the cubical complex K.  The following commands use an algorithm, based on the notion of a discrete vector field,  to find a CW-complex L of the homotopy type of K but involving a total of just 25 cells. (Since H0(K) = Z3 and H1(K) = Z20 this is close to the minimum possible number of cells in any CW-complex having the homotopy type of K.)
gap> L:=DVFReducedCubicalComplex(K);
Non-regular cubical complex of dimension 2 with discrete vector field.

gap> Size(L);
25

gap> C:=ChainComplex(L);
Chain complex of length 2 in characteristic 0 .

gap> Homology(C,0);
[ 0, 0, 0 ]

gap> Homology(C,1);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
4. Permutahedral Complexes
Euclidean n-space can be tessellated by regular n-dimensional permutahedra. By a pure permutahedral complex we mean a union of finitely many of the permutahedra in this tessellation. Using the HAPPermutahedral package written by Fintan Hegarty we can represent the above black an white image as a pure permutahedral complex P. Although we are not guaranteed that the homotopy type of the pure permutahedral complex P is identical to that of the above pure cubcial complex representing the image, though we would hope that the homotopy types of the two complexes are not too dissimilar.

The following commands construct a homotopy retract of P, and then construct the Cech complex NP (which is defined as in the case of pure cubical complexes). An advantage of pure permutahedral complexes over pure cubical complexes is that a pure permutahedral complex of dimension n has Cech complex of the same dimension.
gap> P:=PurePermutahedralComplex(image!.binaryArray);
Pure Permutahedral Complex of dimension 2.

gap> ContractPurePermutahedralComplex(P);

gap> NP:=PureComplexToSimplicialComplex(P,5);
Simplicial complex of dimension 2.

gap> Homology(D,0);
[ 0, 0, 0 ]

gap> Homology(NP,1);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
By contrast, the Cech complex of the pure cubical representation of the black and white image is a simplicial complex of dimension  3.
5. Regular CW-complexes
Simplicial, cubical and permutahedral complexes are all examples of regular CW-spaces. Since some homotopical algorithms are best implemented in the general setting of regular CW-spaces the HAP package proides a data type for this general setting.

The following example creates a 4-dimensional pure cubical complex T representing a standard torus.  It then  computes the Cech complex NT which is a 15-dimensional simplicial complex. It then converts the data type of NT into that of a regular CW-somplex. This CW-complex Y involves a total of 1172776 cells.
gap> Circle:=PureCubicalComplex([[1,1,1,1,1],[1,1,0,1,1],[1,1,1,1,1]]);
Pure cubical complex of dimension 2.

gap> T:=DirectProductOfPureCubicalComplexes(Circle,Circle);
Pure cubical complex of dimension 4.

gap> NT:=CechComplexOfPureCubicalComplex(T);
Simplicial complex of dimension 15.

gap> Y:=SimplicialComplexToRegularCWSpace(NT);
Regular CW-space of dimension 15

gap> Size(Y);
1172776
The 15-dimensional CW-space Y has 1172776 cells. However, we know from its construction that it has the homotopy type of a torus. The following commands compute a set of "critical cells" for Y which can be used to build a smaller non-regular CW-complex of the same homotopy type. The computation shows that there is a CW-complex of the same homotopy type involving just one 0-cell, two 1-cells and one 2-cell.  
gap> CriticalCellsOfRegularCWSpace(Y);
[ [ 2, 5872 ], [ 1, 1116 ], [ 1, 2017 ], [ 0, 196 ] ]
The following command computes the chain complex of the space whose cells correspond to the critical cells of Y.
gap> C:=ChainComplex(Y);;

gap> List([0..15],C!.dimension);
[ 1, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
6. Homotopy Equivalent Pure Cubical Complexes
It often happens that, for a given pure cubical complex X, any pure cubical homotopy retract R of X is necessarily quite large. Smaller homotopy equivalent pure cubical complexes ZR can often be obtained by allowing zig-zag sequences of homotopy retracts.

X ----> Y1 <---- Y2 ----> Y3 <---- Y4 ----> ... <--- ZR

To illustrate the benefit of this approach we consisder the suspension S of the above black and white image. The pure complex S has 182727 facets. Our algorithm for finding a homotopy retract of S produces a homotopy retract R with 29809 facets. Our algorithm for finding a zig-zag homotopy equivalent complex produces a homotopy equivalent pure cubcial complex ZR with just 304 facets.

Finally, we produce the cellular chain complex of a non-regular CW-complex V of the homotopy type of S. The CW-complex V has one 0-cell, two 1-cells and twenty 2-cells. This is the minimum possible number of cells for any CW-complex of the homotopy type of S.
gap> image:=ReadImageAsPureCubicalComplex("bw_image.bmp",400);

gap> X:=SuspensionOfPureCubicalComplex(image);
Pure cubical complex of dimension 3.

gap> Size(X);
182727

gap> R:=ContractedComplex(X);
Pure cubical complex of dimension 3.

gap> Size(R);
29809

gap> ZR:=ZigZagContractedPureCubicalComplex(S);
Pure cubical complex of dimension 3.

gap> Size(ZR);
304

gap> V:=DVFReducedCubicalComplex(PureCubicalComplexToCubicalComplex(ZR));
Non-regular cubical complex of dimension 3 with discrete vector field.

gap> C:=ChainComplex(V);
Chain complex of length 3 in characteristic 0 .

gap> C!.dimension(0);
1
gap> C!.dimension(1);
2
gap> C!.dimension(2);
20
gap> C!.dimension(3);
0
Previous Page
 Contents
 Next page