AboutHap

About HAP: Davis Complex

Davis Complex
Sub-package by Alexander D. Rahm and Ruben J. Sanchez-Garcia

The aim of this subpackage is to create a combinatorial model of the Davis complex of an arbitrary Coxeter group.
The Davis complex has been defined in [M.W. Davis, Groups generated by reflections, Ann. Math. 117 (1983)]; and the present sub-package is a release of the implementation described in [R.J. Sanchez-Garcia, Equivariant K-homology for some Coxeter groups, J. London Math. Soc. (2) 75 (2007)].
A Coxeter group is represented by a Coxeter matrix M, with entries the order of the elements s_i s_j in a Coxeter presentation (the generators s_i are of order 2). Since the diagonal elements are one, and it is symmetric, we only need to specify the elements above (or below) the diagonal.

The function CreateCoxeterMatrix allows to convert the information of a Coxeter diagram into a Coxeter matrix. For example, consider a Coxeter triangle group, generated by elements s_1, s_2, s_3 of order 2. Let us consider the special case where the order of s_1 s_2 is 2, and the orders of s_1 s_3 and s_2 s_3 are 4:

gap> M:= CreateCoxeterMatrix( 3, [2,4,4] );
[ [ 1, 2, 4 ], [ 2, 1, 4 ], [ 4, 4, 1 ] ]

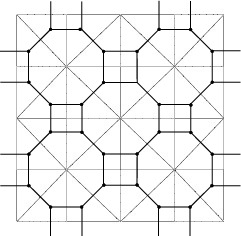
This Coxeter matrix specifies the Coxeter triangle group acting on the following tessellation:

The sub-package constructs the Davis complex for this group:

gap> C := DavisComplex(M);
Non-free resolution in characteristic 0 for matrix group with 3 generators.
No contracting homotopy available.

The function DavisComplex takes a Coxeter matrix as input, and creates the Davis complex as a HAP ContractibleGComplex data type. This is a simplicial complex with one n-simplex for each strictly increasing chain of spherical subsets of length n+1. A spherical subset is a subset of the Coxeter generators that generates a spherical (finite) Coxeter subgroup. The group acts by conjugation on the chains; and for instance the stabiliser of an n-simplex is the group generated by the first (or smallest) spherical subgroup in the chain. For more details, see [M.W. Davis, Groups generated by reflections, Ann. Math. 117 (1983)] or [R.J. Sanchez-Garcia, Equivariant K-homology for some Coxeter groups, J. London Math. Soc. (2) 75 (2007)].

Then, the core functions of HAP can be applied in order to obtain the group homology of our Coxeter group:

gap> q := 5;; F:= FreeGResolution(C,q);
Resolution of length 5 in characteristic 0 for matrix group with 3 generators.
No contracting homotopy available.

gap> T := TensorWithIntegers(F);
Chain complex of length 5 in characteristic 0 .

gap> for n in [0..q-1] do Print(Homology(T,n),"\n"); od;
[ 0 ]
[ 2, 2, 2 ]
[ 2, 2, 2 ]
[ 2, 2, 2, 2, 4, 4 ]
[ 2, 2, 2, 2, 2, 2 ]

As well, the Bredon homology of the Coxeter groups, with respect to the family of finite subgroups and coefficients in the complex representation rings (interesting in light of the Baum-Connes conjecture), can be computed from the Davis complex using the Bredon homology functions of HAP.

A simpler example is the 3-dihedral group:

gap> M:= CreateCoxeterMatrix( 2, [3] );
[ [ 1, 3 ], [ 3, 1 ] ]

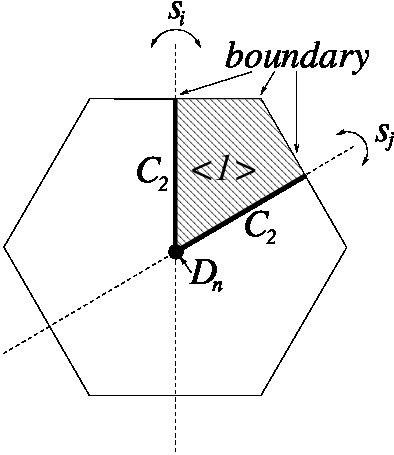
The Coxeter cell for the 3-dihedral group looks like this:

The sub-package constructs the Davis complex for this group:

gap> C := DavisComplex(M);
Non-free resolution in characteristic 0 for Group( [ [ [ -1, 1 ], [ 0, 1 ] ], [ [ 1, 0 ], [ 1, -1 ] ] ]) .
No contracting homotopy available.

Then, the core functions of HAP can be applied in order to obtain the group homology of our Coxeter group:

gap> q := 5;; F:= FreeGResolution(C,q);
Resolution of length 5 in characteristic 0 for Group( [ [ [ -1, 1 ], [ 0, 1 ] ], [ [ 1, 0 ], [ 1, -1 ] ] ]) .
No contracting homotopy available.

gap> T := TensorWithIntegers(F);
Chain complex of length 5 in characteristic 0 .

gap> for n in [0..q-1] do Print(Homology(T,n),"\n"); od;
[ 0 ]
[ 2 ]
[ ]
[ 6 ]
[ ]

We can recover the above result "by hand" by elementary methods of group homology.

An example where the infinite orders (represented by zeros) appear in the Coxeter matrix, is:

gap> M:= CreateCoxeterMatrix(3,[0,0,0]);
[ [ 1, 0, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ]

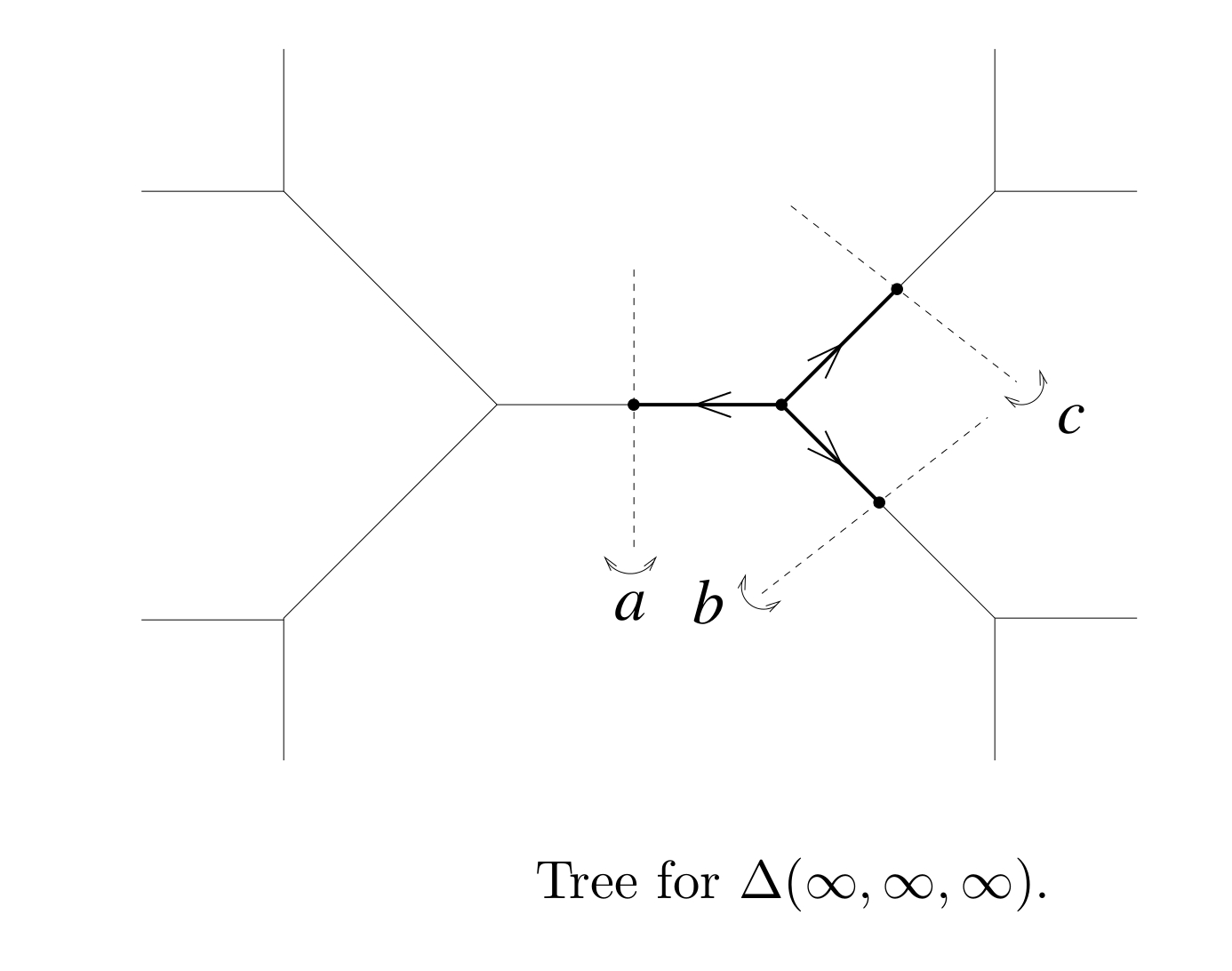
This Coxeter group acts freely on the infinite trivalent tree (where we set a := s_1, b := s_2, c := s_3):

The sub-package constructs the Davis complex for this group:

gap> C := DavisComplex(M);
Non-free resolution in characteristic 0 for matrix group with 3 generators.
No contracting homotopy available.

Then, the core functions of HAP can be applied in order to obtain the group homology of our Coxeter group:

We conclude with an example where the infinite orders (represented by zeros) mix with finite orders of products in the Coxeter matrix.

gap> M:= CreateCoxeterMatrix(3,[2,2,0]);
[ [ 1, 2, 2 ], [ 2, 1, 0 ], [ 2, 0, 1 ] ]

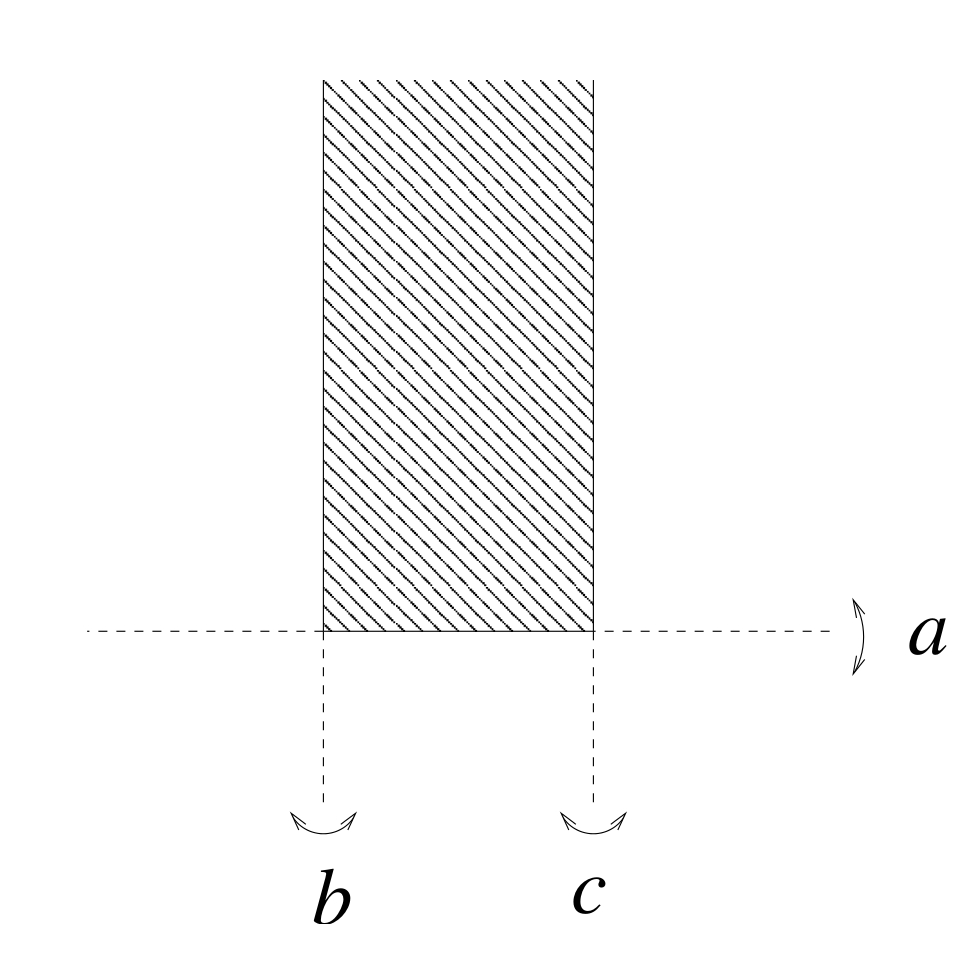
A Coxeter cell for this Coxeter group looks as follows (where we set a := s_1, b := s_2, c := s_3):

The sub-package constructs the Davis complex for this group:

gap> C := DavisComplex(M);
Non-free resolution in characteristic 0 for matrix group with 3 generators.
No contracting homotopy available.

Then, the core functions of HAP can be applied in order to obtain the group homology of our Coxeter group:

More interesting examples can be computed with the present subpackage on the Coxeter tetrahedral groups (with four generators in the Coxeter matrix). This has been carried out as a check for the calculations in [A. Rahm, Accessing the cohomology of discrete groups above their virtual cohomological dimension, Journal of Algebra].

Contents