Previous
 About HAP: Graphs of Groups, Fuchsian groups and Kleinian groups
 next

Graphs of groups
A graph of groups is a connected graph Y together with
  • groups Gv and Ge where v and e range respectively over the vertices and edges of Y,
  • and monomorphisms s:Ge→Gv and t:Ge→Gw for every edge e, where v and w are the vertices of e.
The fundamental group of a graph of groups is defined using a notion of "path" where an element of Gv is regarded as a path from v to v; one imposes the relations

s(a) e = e t(a)

for every a in Ge . That is, the composite paths




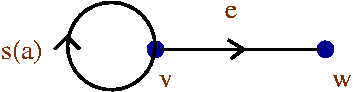
and





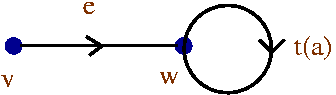
are regarded as equal paths from v to w.
Amalgamated products and HNN extensions can both be viewed as fundamental groups of graphs of groups. For example, the following commands create a graph of groups corresponding to the amalgamated product G=H*AK where H is the symmetric group H=S5 and K is the symmetric group K=S4 . The common subgroup A is the symmetric group A=S3 .

A graph of groups is represented by a list consisting of the vertex groups and pairs of monomorphisms which define edges. Each group must be given a name using the SetName() command, and distinct groups must be given different names.
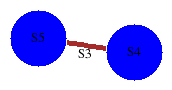
gap> S5:=SymmetricGroup(5);SetName(S5,"S5");;
gap> S4:=SymmetricGroup(4);SetName(S4,"S4");;
gap> A:=SymmetricGroup(3);SetName(A,"S3");;
gap> AS5:=GroupHomomorphismByFunction(A,S5,x->x);;
gap> AS4:=GroupHomomorphismByFunction(A,S4,x->x);;
gap> D:=[S5,S4,[AS5,AS4]];;
gap> GraphOfGroupsDisplay(D);;
The following additional commands create a resolution for the above amalgamated product G and then calculate H7(G,Z) = (Z2)3+Z4+Z60
gap> R:=ResolutionGraphOfGroups(D,8);;
gap> Homology(TensorWithIntegers(R),7);
[ 2, 2, 2, 4, 60 ]
The following commands create a graph of groups corresponding to the HNN extension G=H*A where H is the symmetric group H=S5 and A is the subgroup A=S3 and f:A→S5 is the homomorphism (1,2) → (3,4), (1,2,3) → (3,4,5). The HNN extension G is obtained from H by adding an element t subject to the relations  t-1 a t = f(a) for a in S3.
gap> S5:=SymmetricGroup(5);SetName(S5,"S5");
gap> A:=SymmetricGroup(3);SetName(A,"S3");
gap> f:=GroupHomomorphismByImages(A,S5,[(1,2),(1,2,3)],[(3,4),(3,4,5)]);;
gap> g:=GroupHomomorphismByFunction(A,S5,x->x);
gap> D:=[S5,[f,g]];;
gap> GraphOfGroupsDisplay(D);;
The following additional commands create a resolution for the HNN extension and calculate H7(G,Z) = (Z2)2+Z60 .
gap> R:=ResolutionGraphOfGroups(D,8);;
gap> Homology(TensorWithIntegers(R),7);
[ 2, 2, 60 ]
Fuchsian and Kleinian groups
A Kleinian group is discrete subgroup of PSL(2,C), the full group of orientation preserving isometries of 3-dimensional hyperbolic space. A Fuchsian group is a discrete subgroup of PSL(2,R) and as such acts on the hyperbolic plane. A "fundamental domain" for a Kleinian or Fuchsian group G gives rise to a tessellation of hyperbolic 3- or 2-space. Let X denote the 1-skeleton of this tessellation. Then G acts on X in such a way that no edge is inverted. The quotient graph Y=X/G is thus a graph of groups in which vertices and edges are labelled by the subgroups of G stabilizing the corresponding vertices and edges in Y.

The computational method described in [G. Ellis & A.G. Williams, "On the cohomology of generalized triangle groups", Comment. Math. Helv. 80 (2005), 1-21] can be partially summarized as follows.
Let G be a Fuchsian or Kleinian group. Let Y be the graph of groups arising from G and a fundamental domain. Let P be the fundamental group of Y. Then the "obvious" quotient homomorphism P→G induces an isomorphism

Hn(P,M) → Hn(G,M)

for any ZG-module M and all n>2 (Fuchsian case) or all n>3 (Kleinian case).

As an example consider the classical triangle group defined by the presentation

T = T(l,m,n) = < a, b |  al = bm = (ab-1)n = 1 >

where 1/|l| + 1/|m| + 1/|m| < 1. This group acts on the hyperbolic plane as follows. Let v1 and v2 be distinct point in the hyperbolic plane. Let the generator a of T act as a clockwise rotation about v1 through an angle 2 pi/¦l| , and let the generator b of T act as a clockwise rotation about v2 through an angle 2 pi/¦m| . It follows that (ab-1) acts as an anti-clockwise rotation about some point v3 through an angle 2 pi/|n|. Let v4 be the image of v3 under a reflection in the line v1v2 . Then the points v1 , v2 , v3 , v4 are the corners of a quadrilateral fundamental region for the action of T. The edges of this fundamental region have trivial stabilizer subgroups in G. The vertices v1 , v2 , v3 have cyclic stabilizer subgroups A = <a>, B=<b> and C=<c> respectively.

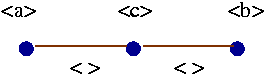
The associated graph of groups is

 

The fundamental group P of this graph has the same homology as the triangle group T(l,m,n) in dimensions greater than 3.

So for example, the following commands show that the triangle group T=T(2,3,4) has 5-dimensional integral homology H5(T,Z) = Z2+Z12 .
gap> a:=(1,2);; b:=(1,2,3);; c:=(1,2,3,4);; f:=();; g:=();;
gap> A:=Group(a);; SetName(A,"A");;
gap> B:=Group(b);; SetName(B,"B");;
gap> C:=Group(c);; SetName(C,"C");;
gap> F:=Group(f);; SetName(F,"F");;
gap> G:=Group(g);; SetName(G,"G");;
gap> FA:=GroupHomomorphismByFunction(F,A,x->x);;
gap> FC:=GroupHomomorphismByFunction(F,C,x->x);;
gap> GC:=GroupHomomorphismByFunction(G,C,x->x);;
gap> GB:=GroupHomomorphismByFunction(G,B,x->x);;
gap> Graph:=[A,B,C,[FA,FC],[GC,GB]];;
gap> GraphOfGroupsDisplay(Graph);;

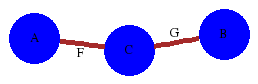
gap> R:=ResolutionGraphOfGroups(Graph,6);;
gap> Homology(TensorWithIntegers(R),5);
[ 2, 12 ]
Previous Page
 Contents
 Next page