Table Of
Contents
 About HAP: Overview
 Next

HAP can be used to make basic calculations in the cohomology of finite and infinite groups. For example, to calculate the integral homology Hn(D201,Z) of the dihedral group of order 402 in dimension n=99 we could perform the following commands.
gap> F:=FreeGroup(2);; x:=F.1;; y:=F.2;;

gap> G:=F/[x^2,y^201,(x*y)^2];; G:=Image(IsomorphismPermGroup(G));;

gap> GroupHomology(G,99);
[ 2, 3, 67 ]

gap> time;
4845
The HAP command GroupHomology(G,n) returns the abelian group invariants of the n-dimensional homology of the group G with coefficients in the integers Z with trivial G-action. We see that H99(D201,Z) = Z402, (Timings are in milliseconds, and most are measured on a 1.4GHz laptop with 256MB memory.)

The above example has two features that dramatically help the computations. Firstly, D201 is a relatively small group. Secondly, D201 has periodic homology with period 4 (meaning that Hn(D201,Z) = Hn+4(D201,Z) for n>0) and so the homology groups themselves are small. 

Typically, the homology of larger non-periodic groups can only be computed in low dimensions. The following commands show that:
  • the alternating group A7 (of order 2520) has H10(A7,Z) = Z6+(Z3)2 ,
  • the special linear group SL3(Z3) (of order 5616) has H8(SL3(Z3),Z) = Z6 ,
  • the Coxeter group B5 (of order  3840), represented by a Coxeter diagram on 5 vertices, has H4(B5,Z) = (Z2)12 .
  • the group K=Ker( SL2(Z53) → SL2(Z5) ) (of order 15625) has H3(K,Z) = (Z5)6+Z125. (This reproduces a calculation of W.Browder and J.Pakianathan which was used to  produce a counter-example to a conjecture of A. Adem.)
  • the abelian group G=C2×C4×C6×C8×C10 ×C12 (of order 46080) has H6(G,Z) = (Z2)280+(Z4)12+(Z12)3 .
  • the Mathieu simple group M23 (of order 10200960) has H2(M23,Z) = H3(M23,Z) = H4(M23,Z) = 0; this reproduces J. Milgram's counter-example to a conjecture of J.-L. Loday. Furthermore, we get the new result that H5(M23,Z) = Z7.
  • The Mathieu simple group M24 (of order 244823040) has H3(M24,Z) = Z12 and H4(M24,Z) = 0.
gap> GroupHomology(AlternatingGroup(7),10);time;
[ 2, 3, 3, 3 ]
1756

gap> S:=Image(IsomorphismPermGroup(SL(3,3)));;
gap> GroupHomology(S,8);time;
[ 2, 3 ]
6340

gap> B5:=[[1,[2,3]],[2,[3,3]],[3,[4,3]],[4,[5,4]]];;
gap> GroupHomology(["Coxeter",D],4);time;
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
56240

gap> K:=MaximalSubgroups(SylowSubgroup(SL(2,Integers mod 5^3),5))[2];
gap> K:=Image(IsomorphismPcGroup(K));
gap> GroupHomology(K,3);time;
[ 5, 5, 5, 5, 5, 5, 125 ]
3254

gap> G:=AbelianGroup([2,4,6,8,10,12]);;
gap> GroupHomology(G,6);time;
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 12, 12, 12 ]
23265

gap> GroupHomology(MathieuGroup(23),2);time;
[  ]
9395
gap> GroupHomology(MathieuGroup(23),3);time;
[  ]
157961
gap> GroupHomology(MathieuGroup(23),4);time;
[  ]
276853
gap> GroupHomology(MathieuGroup(23),5);time;
[ 7 ]
20639802

gap> GroupHomology(MathieuGroup(24),3);time;
[ 4, 3 ]
3205565

gap> GroupHomology(MathieuGroup(24),4);
[  ]
The command GroupHomology() returns the mod p homology when an optional third argument is set equal to a prime p. The following shows that the Sylow 2-subgroup P of the Mathieu simple group M24 has 6-dimensional mod 2 homology H6(P,Z2)=(Z2)143 . (The group P has order 1024 and the computation took over two hours to complete.)
gap> GroupHomology(SylowSubgroup(MathieuGroup(24),2),6,2);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
The mod 2 cohomology ring H*(G,Z2) can be calculated for smallish 2-groups G using the HAPprime extension package (which uses the Singular system for commutative algebra). For instance, the following commands compute a presentation and Poincare series for this ring when G is the Sylow 2-subgroup of the Mathieu group M12 . The commands use the Lyndon-Hochschild-Serre spectral sequence and Groebner bases to verify that the computations are correct.
gap> G:=SylowSubgroup(MathieuGroup(12),2);;

gap> Mod2CohomologyRingPresentation(G);
Graded algebra GF(2)[ x_1, x_2, x_3, x_4, x_5, x_6, x_7 ] /
[ x_2*x_3, x_1*x_3, x_3*x_4, x_1*x_2^2+x_2^3+x_2*x_5, x_1*x_2*x_5+x_2*x_6,
  x_1^2*x_4+x_2^2*x_4+x_2^2*x_5+x_1*x_6+x_4^2+x_4*x_5,
  x_1^3*x_2+x_2^4+x_1*x_2*x_4+x_2^2*x_4+x_2^2*x_5+x_1*x_6+x_2*x_6+x_4*x_5,
  x_1*x_4*x_5+x_4*x_6, x_2^3*x_5+x_2^2*x_6+x_2*x_5^2,
  x_1*x_5*x_6+x_3^2*x_7+x_3*x_5*x_6+x_6^2,
  x_2^2*x_4*x_5+x_2^2*x_5^2+x_1*x_4*x_6+x_3^2*x_7+x_3*x_5*x_6+x_4^2*x_5+x_4*x_\
5^2+x_6^2, x_2^2*x_4^2+x_2^2*x_5^2+x_2*x_4*x_6+x_2*x_5*x_6,
  x_1^2*x_2*x_6+x_2^3*x_6+x_2^2*x_5^2+x_1*x_4*x_6+x_2*x_4*x_6+x_2*x_5*x_6+x_4^\
2*x_5 ] with indeterminate degrees [ 1, 1, 1, 2, 2, 3, 4 ]
gap> time;
19685

gap> G:=SylowSubgroup(MathieuGroup(12),2);;
gap> PoincareSeriesLHS(G);
(1)/(-x_1^3+3*x_1^2-3*x_1+1)
gap> time;
11757
The homology of certain infinite groups can also be calculated. The following commands show that
  • the 99-dimensional integral homology of SL2(Z[1/7]) is H99(SL2(Z[1/7]),Z) = Z4 + Z12. (This homology was first calculated by A. Adem and N. Naffah).
  • the 4-dimensional integral homology of SL3(Z) is H4(SL3(Z),Z) = Z2. 
  • the 6-dimensional integral homology of the Bianchi group SL2(Z[w]) with w2=-2 is H6(SL2(Z[w]),Z) = Z2.
  • the classical braid group B on eight strings (represented by a linear Coxeter diagram D with seven vertices) has 5-dimensional integral homology H5(B,Z) = Z3 .
  • the amalgamated product G=S5*AS4 of the symmetric groups S5 and S4 over the canonical subgroup A=S3 has 5-dimensional integral homology H5(G,Z) = (Z2)5 . (The amalgamated product can be represented as a graph of groups.)
  • the Heisenberg group H in five complex variables (a torsion free nilpotent group of class two) has 5-dimensional integral homology H5(H,Z) = (Z2)43+Z6+Z132.
  • the free nilpotent group N of class 2 on four generators has 4-dimensional integral homology H4(N,Z) = (Z3)4+Z84. (The full range of homology groups for N were first calculated in a paper by L. Lambe.)
  • The 3-dimensional crystallographic space group S with Hermann-Mauguin symbol "P62" has 5-dimensional integral homology H5(S,Z) = Z2+Z2.
(The last three examples require the "AClib", "Polycyclic" and "nq" packages. HAP can be loaded without these packages if such examples are not required..)
gap> R:=ResolutionSL2Z(7,100);
Resolution of length 100 in characteristic 0 for SL(2,Z[1/7]) .
No contracting homotopy available.
gap>  Homology(TensorWithIntegers(R),99);
[ 4, 12 ]


gap> C:=ContractibleGcomplex("SL(3,Z)");;
gap> R:=FreeGResolution(C,5);;
gap> Homology(TensorWithIntegers(R),4);
[ 2 ]


gap> C:=ContractibleGcomplex("SL(2,Z[sqrt(-2)])");;
gap> R:=FreeGResolution(C,7);;
gap> Homology(TensorWithIntegers(R),6);
[ 2 ]


gap> D:=[  [1,[2,3]],  [2,[3,3]],  [3,[4,3]],  [4,[5,3]],  [5,[6,3]],  [6,[7,3]]  ];;
gap> CoxeterDiagramDisplay(D);;

gap> GroupHomology(D,5);time;
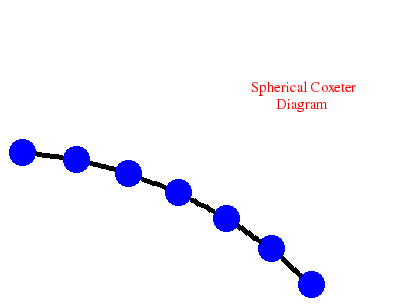
[ 3 ]
13885



gap> S5:=SymmetricGroup(5);SetName(S5,"S5");
gap> S4:=SymmetricGroup(4);SetName(S4,"S4");
gap> A:=SymmetricGroup(3);SetName(A,"S3");
gap> AS5:=GroupHomomorphismByFunction(A,S5,x->x);
gap> AS4:=GroupHomomorphismByFunction(A,S4,x->x);
gap> D:=[S5,S4,[AS5,AS4]];
gap> GraphOfGroupsDisplay(D);

gap> GroupHomology(D,5);time;
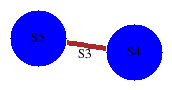
[ 2, 2, 2, 2, 2 ]
22004


gap> GroupHomology(HeisenbergPcpGroup(5),5);time;
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0 ]
73765


gap> F:=FreeGroup(4);; N:=NilpotentQuotient(F,2);;
gap> GroupHomology(N,4);time;
[ 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
41967


gap> GroupHomology(SpaceGroupBBNWZ("P62"),5);time;
[ 2, 2 ]
4336
The command GroupHomology(G,n) is a composite of several more basic HAP functions and attempts, in a fairly crude way, to make reasonable choices for a number of parameters in the calculation of group homology. For a particular group G you would almost certainly be better off using the more basic functions directly and making the choices yourself! Similar comments apply to functions for cohomology (ring) calculations.

The subsequent pages of this manual explain the basic HAP functions. The intending reader should be aware that many of the examples are intended to illustrate the full potential of HAP and  consequently may take many minutes (and in one or two cases hours) to run.
For a given crystallographic space group S the HAPcryst extension (which uses the Cryst GAP package and the Polymake computational geometry system) can be used to compute a fundamental cell which tiles euclidean space in such a way that the tiling is respected by the action of S. For instance, the following commands compute a fundamental cell for the 3-dimensional space group S with Hermann-Mauguin symbol "P62" and exhibit the 1-skeleton of this cell.
gap> fd:=FundamentalDomainStandardSpaceGroup([1/2,1/3,1/5],SpaceGroupBBNWZ("P62"));;
gap>  Polymake(fd,"VISUAL_GRAPH");
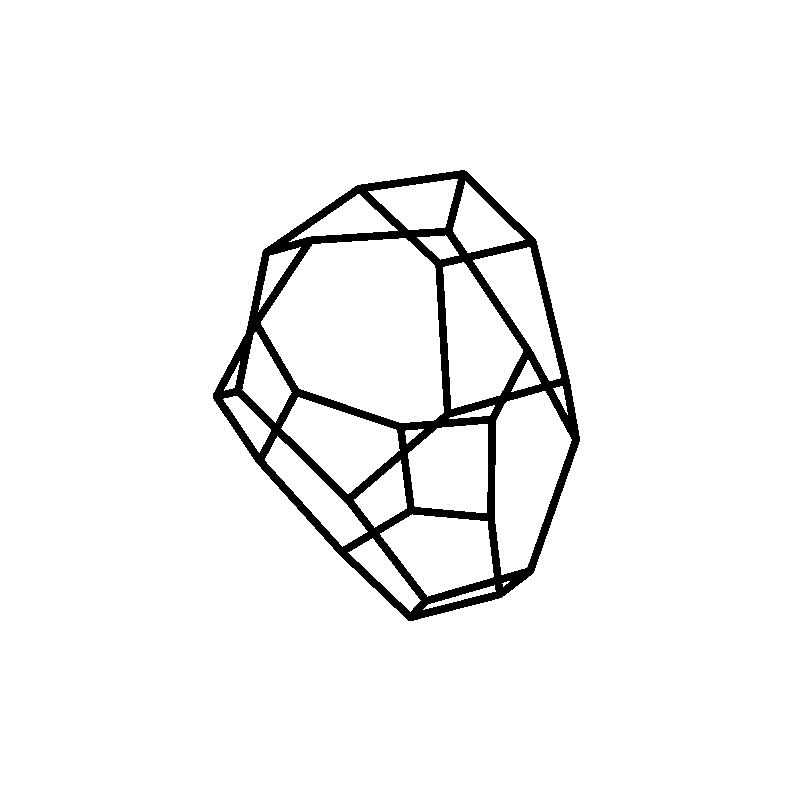
We end this introduction by mentioning that HAP can also be used to make calculations such as:
  • The rank of the mod 2 cohomology group Hk(M11,Z2) of the Mathieu group M11 of order 7920 is equal to the coefficient of xk in the Poincare series  p(x) = (x4-x3+x2-x+1)/(x6-x5+x4-2x3+x2-x+1)  for all k less than 15. (This Poincare series for the ring H*(M11,Z2) was first calculated in [P.Webb, "A local method in group cohomology", Comm. Math. Helv. 62 (1987) 135-167]. )
  • The mod 2 cohomology ring H*(D32,Z2) for the dihedral group of order 64 is generated by two elements of degree 1 and one element of degree 2 and possibly (though not very likely) some generators of degree greater than 30.
  • The Lie algebra M3(Z) of all integer 3×3 matrices has 5-dimensional Lie homology H5(A,Z)=(Z2)8+Z.
  • The suspension X=SK(G,1) of an Eilenberg-Mac Lane space for the free nilpotent group G of class 2 on four generators has third homotopy group pi3X = Z30 .
  • The double suspension Y=SSK(G,1) of an Eilenberg-Mac Lane space for the group G=GL(4,3) of 4×4 matrices over the field of three elements (of order 24261120) has fourth homotopy group pi4Y = Z2 .
  • The free nilpotent Lie algebra A of class two on four generators, over the ring of integers Z, has 3-dimensional Leibniz homology HL3(A,Z)=(Z2)8 + (Z6)16 +Z176 .
  • The group presentation P = <x,y,z,a,b,c, | a=xy, b=yz, c=zx, ax=ya, by=zb, cz=xc > is aspherical.
  • The 3-dimensional module M over the field F of two elements, arising from the canonical left action of the group G=GL3(2) of 3×3 matrices (of order 168), has a 2-dimensional fifth Ext module Ext5FG(M,F)=F2.
  • The  3-dimensional integral homology of the  homotopy 2-type X represented by the automorphism crossed module  D16 --> Aut(D16) is H3(X,Z)=Z2+Z2+Z4.
The following commands yield these seven calculations.
gap> PoincareSeriesPrimePart(MathieuGroup(11),2,14);
(x^4-x^3+x^2-x+1)/(x^6-x^5+x^4-2*x^3+x^2-x+1)

gap> H:=ModPCohomologyGenerators(DihedralGroup(64),30);;
gap> List(H[1], H[2]);
[ 0, 1, 1, 2 ]

gap>  A:=MatLieAlgebra(Integers,3);;
gap>  LieAlgebraHomology(A,5);
[ 2, 2, 2, 2, 2, 2, 2, 2, 0 ]

gap>  F:=FreeGroup(4);;G:=NilpotentQuotient(F,2);;
gap>  ThirdHomotopyGroupOfSuspensionB(G);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0 ]

gap> G:=Image(IsomorphismPermGroup(GL(4,3)));;
gap> NonabelianSymmetricKernel_alt(G);
[ [  ], [ 2 ] ]

gap> F:=FreeGroup(4);;G:=NilpotentQuotient(F,2);;
gap> L:=LowerCentralSeriesLieAlgebra(G);;
gap> LeibnizAlgebraHomology(L,3);
[ 2, 2, 2, 2, 2, 2, 2, 2, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

gap> F:=FreeGroup(6);;x:=F.1;;y:=F.2;;z:=F.3;;a:=F.4;;b:=F.5;;c:=F.6;;
gap> rels:=[a^-1*x*y, b^-1*y*z, c^-1*z*x, a*x*(y*a)^-1, b*y*(z*b)^-1, c*z*(x*c)^-1];;
gap> IsAspherical(F,rels);;
Presentation is aspherical.

gap> M:=GModuleByMats(GeneratorsOfGroup(GL(3,2)),GF(2));;
gap> R:=ResolutionFpGModule(DesuspensionMtxModule(M),5);;
gap> Cohomology(HomToIntegersModP(R,2),4);
2

gap> C:=AutomorphismGroupAsCatOneGroup(DihedralGroup(32));;
gap> N:=NerveOfCatOneGroup(C,4);;
gap> K:=ChainComplexOfSimplicialGroup(N);;
gap> Homology(K,3);
[ 2, 2, 4 ]

                
Contents
 Next page