|
Contact us!
Tel: (519) 672-7990
|

Mathcamp 2002 Application Quiz
Instructions
Try to solve as many of these problems as you can. We certainly don't expect every applicant to solve every problem on the quiz - we often accept people who can do only six, or even fewer - but we do want you to give all the questions some thought. Some of them may be tougher than you're used to. Keep turning them over in your head: often the crucial insight comes when you least expect it!
You are welcome to use outside resources, such as books or the Web, as long as you acknowledge and reference them. Of course, all the actual work must be your own. Remember that your reasoning matters more to us than your final answers, so justify all your assertions, and don't hesitate to submit partial solutions.
Good luck, and have fun!
Problems
-
In a certain game, there are three piles of stones: one with 22
stones, one with 14 stones, and one with 12 stones. At each turn, you can
double the number of stones in a pile by transferring stones to it from
one other pile. (For example, your first move can be to transfer 12 stones
from the first pile to the third pile.) The game ends if the three piles
are equal in size. Can you find a way to end the game in three moves?
-
Imagine a corridor with 2002 light switches. Initially, all the lights
are off. Then 2002 people walk through the corridor, one after the other.
The first person flips every switch, the second person flips every other
switch (starting with the second), the third person flips every third
switch (starting with the third), and so on. After all the people have
gone through, which lights are on and which are off?
-
Show that you cannot cover a circular disk with two circular disks of
smaller diameter.
-
Three bugs are crawling on the coordinate plane. They move one at a
time, and each bug will only crawl in a direction parallel to the line
joining the
other two.
-
If the bugs start out at (0,0), (3,0), and (0,3), is it possible that
after some time the first bug will end up back where it started, while the
other two bugs switch places?
- Can the three bugs end up at (1,2), (2,5), and (-2,3)?
-
If the bugs start out at (0,0), (3,0), and (0,3), is it possible that
after some time the first bug will end up back where it started, while the
other two bugs switch places?
-
Suppose 15 pennies are arranged in a triangle, as in the following
diagram:
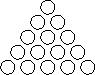
-
The decimal expansion of the fraction 1/11 = .090909... consists
of the two digits 09 repeating over and over; we say that this
decimal expansion has period length 2. Similarly, the decimal
expansion of 1/37 = .027027027... has period length 3. Can you
find other integers n such that the decimal expansion of
1/n has period length 2? period length 3? Can you find all the
prime numbers p such that the decimal expansion of 1/p has
period length 6 or less? Can you find any prime numbers p so that
the octal (i.e., base 8) expansion of 1/p has period length 3?
-
You are a secret agent assigned to carry out classified research on
Enemy Government Gadgets (EGGs). Your mission: to determine the
highest floor of an office building from which a dropped EGG will survive
falling to the ground. Your method: drop an EGG from different floors
and see if it breaks.
-
The budget is tight at the agency, so you'll only have one EGG to work
with. Once that EGG breaks, that's it. How can you determine the highest
floor that is safe for EGG dropping? Are there any other strategies?
-
Your department has realized the importance of your mission, and has
stretched the budget to allow for 2 EGGs. However, time is of the essence
so you must guarantee that you can finish your mission within 10 drops.
What is the tallest building for which you can be assured of getting a
precise answer, even with the worst possible luck?
- Generalize the problem: if the agency gives you 2 EGGs, and you are allowed k trials, what is the tallest building that you can analyze? What if you are allowed k trials with 3 EGGs? What about k trials with n EGGs?
-
The budget is tight at the agency, so you'll only have one EGG to work
with. Once that EGG breaks, that's it. How can you determine the highest
floor that is safe for EGG dropping? Are there any other strategies?
- (Proposed by Taktin Oey, student, Mathcamp 2001.) A computer is
programmed in the following way. First it prints a random digit between
0 and 9 (with equal likelihood for each possible digit). Then it picks
between the commands "break" and
"continue", again randomly with equal probability. If it picks
"continue", the process repeats; if it
picks "break", the program terminates. What is the probability that the
final output is a palindrome? (For example, if the program runs as "0,
continue, 1, continue, 3, continue, 3, continue, 1, continue, 0, break",
then the output is 013310. It reads the same forward and
backward, and is thus a palindrome.)
-
The Seven Dwarfs are having breakfast, and Snow White has just poured
them some milk. Before drinking, the dwarfs have a ritual. First, Dwarf
#1 splits his milk equally among his brothers' mugs (leaving himself with
nothing). Then Dwarf #2 does the same with his milk, etc. The process
continues around the table, until Dwarf #7 has distributed his milk in
this way. At the end, each dwarf has exactly the same amount of milk as he
started with! If the total amount of milk was 42 ounces, how much milk did
each dwarf have at the beginning? Is this the only possible distribution
of milk, or does the problem admit multiple solutions? (Be sure to justify
your answer.)
-
A single peg is placed at the bottom left-hand corner of a grid that
extends infinitely far up and to the right. You play a game in which you
are allowed to make the following move: if the hole immediately above and
the hole immediately to the right of a peg are both empty, you can remove
the existing peg and place pegs in those two holes instead. Below are some
sample moves.
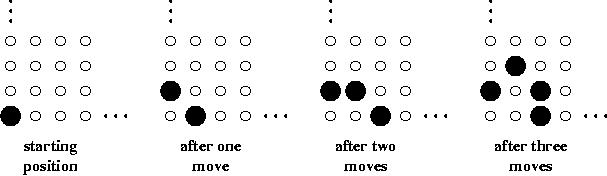
-
Show that, no matter how you move, you can never remove all the pegs
from the 3-by-3 square at the bottom left-hand corner of the grid.
-
Is it possible to remove all the pegs from the six holes closest to
the bottom left-hand corner of the grid (the region indicated in the
picture below)?
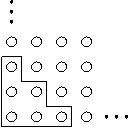
-
Show that, no matter how you move, you can never remove all the pegs
from the 3-by-3 square at the bottom left-hand corner of the grid.