$ \begin{titlepage} \begin{center} \vspace*{1cm}

    \textbf{Real Time Machine Learning Techniques for Wireless Techniques}

    \vspace{0.5cm}
    Thesis Subtitle

    \vspace{1.5cm}

    \textbf{Charles Meyers}

    \vfill

    \vspace{0.8cm}

    Applied Math\
    NYCCT\\
    5/23/2018

\end{center}

\end{titlepage} $

Back Ground Information

Signal Processing

To even begin how to model a signal at a given point of space and time, we have to start with the model of the signal itself. All signals can be modelled as the sum of a series of cosines and sines. In the simplest case:

For a continuous variable $E(t)$, we can model field strength as

$ E(t) = \sum_{i=1}^N |a_i| \cos(2*pi*f_c t+\phi)$

Where $A_{Tx}$ is the amplitude at the transmitter, $f_c$ is the center frequency and $\phi$ is a phase shift. As we can see from the above equation, that only three parameters are within our control: amplitude, frequency, and phase. With these three parameters, there are many modulation schemes. The simplest case is show below in Figure 1.

Figure 1. - Different Modulation Techniques.

$A_{Tx} \cos(2*\pi*f_c t+\phi)$

where $a_i$ is the average amplitude of the signal strength at the receiver, given by the root-mean square estimation.

Modern wi-fi systems (since 802.11n) have deployed MIMO antenna arrays that allow for a particular type of modulation that exploits the phase and amplitude characteristics of signal, called Quadrature Amplitude Modulation (QAM). This is where we must recall Euler's Identity

$e^{i*\pi}+1=0$

If we decompose this according to a basic trigonometric identity and let $x = 2*\pi*f_c t+\phi$, we see that

$e^{i*\pi} = - (\sin^2(\omega)+\cos^2(x))$

Without loss of generality, the above identity holds true for any scaling factor $E$. If we rewrite this in terms of phase and quadratur components we find that

$E(t) = I(t)*\cos(2*pi*f_c t+\phi)+Q(t)-\sin(2*pi*f_c t+\phi)$

where $Q$ is the phase of the signal and $I$ is its amplitude.

Figure 2. - Phase-Amplitude Model.

Furthermore, since phase is a continuous variable, our sample space (as a function of $\theta$ can become arbitrarily small. However, there is a trade-off here. As we decrease our $\theta$ sampling window, we increase our effective noise floor, as each pizza-shaped slice of our measurement window contains the same information in less geometric space. The effect of this is to transmit for bits per symbol. Note this only applies to receiving systems with a single antenna.

Modulation	Bits per Symbol	Symbol Rate	Minimum SNR
BPSK	2	1/2 bit rate	3.5dB
QPSK	3	1/3 bit rate	22.45
8PSK	4	1/3 bit rate	26.96
16QAM4	5	1/4 bit rate	30.67
32QAM	5	1/5 bit rate	32.49
64QAM	6	1/6 bit rate	35.02

http://www.ni.com/tutorial/4805/en/ http://www.scielo.org.za/scielo.php?script=sci_arttext&pid=S0038-23532011000100012

Design Constraints

Previous Models

Friis Equation

In the simplest scenario, we can model the free space path loss. This function of received power in terms of distance is known as Friis' Law:

$P_{Rx}(d)=P_{Tx}G_{Tx}G_{Rx}(\frac{\lambda}{4*\pi*d})^2A_{Rx}$
Where $P$ is the power, $G$ is the gain, and $A$ is the area of the receiving antenna, $d$ is distance between the transmitters and $\lambda$ is the frequency. This equation only applies for systems that are separated by at least one Rayleigh distance defined by

$d_{R}=\frac{2{L_a}^2}{\lambda}$ This is known as the far field. When dealing with link budgets, it is best to use a logarithmic scale because signal levels will vary across many orders of magnitude.

$P_{Rx}(d)=P_{Tx}G_{Tx}G_{Rx}20\log(\frac{\lambda}{4*\pi*d})^2A_{Rx}$ if and only if the powers and gains are consistently in dB or dBm.

Kirchoff Theory

In the same way that Rayleigh distance defines the breaking point of Friis system, Rayleigh roughness can be thought of as the

Perturbation Theory

Log-Distance Path Loss Model

The next model, log-normal shadowing can be thought of as an extension of the Friis model with the added inclusion of a random variable. If the receiver is in the far field of the receiver (where $d>d_R$), $PL(d_0)$ is the path loss measured at a distance $d_0$ from teh transmitter, then the path loss when moving from distance $d0$ to $d$ is given by the equation

$PL{d_0\rightarrow d}(dB) PL(d_0)+10n\log_{10}\frac{d}{d_0} + \chi_1$c where $n$ is the path loss exponent, given by the table below and $\chi$ is a zero mean random normal distribution.

https://www.gaussianwaves.com/2013/09/log-distance-path-loss-or-log-normal-shadowing-model/

Environment	Path Loss Exponent min	Path Loss Exponent Max
Free Space	2	2
Urban area cellular radio	2.7	3.5
Shadowed urban cellular radio	3	5
Inside-LoS	1.6	1.8
Obstructed in building	4	6
Obstructed in Factory	2	3

Figure 1: Empirical Log-distance coefficients

Noise

In most circumstances it is too cumbersome to describe all the sources of noise. If it wasn't, then we'd solve Maxwell's Equations within the system and be done with it. However there are many sources of interference. Multipath propagation is a big limitation to predicting the shape of a wireless network in an urban space as different rays from the transmitter bounce around the room and reach the receiver at different times. Because receivers cannot distinguish the 'true' signal from the multi-path signal, the receiver just adds the components of those multipaths up, creating interference. This interference can be constructive or destructive. Small-scale fading occurs when a user is moving--when the user moves further away, they increase the phase and possibly the measured voltage level. Additionally, the transmitter and receiver each produce noise. The total power due to noise can be described as

$P = (\sum_{k=0}^{n}(x_I+x_Q))^2$ Where $x_I$ and $x_Q$ are linearly independent vectors of amplitude, $I$, and phase, $Q$. The signal to noise ratio can be expressed as $SNR = \frac{P_{signal}}{P_{noise}}$

where P is the average power measured at the equivalent points in a system and within the same system bandwidth. If we include interference, the SNR becomes SINR or the signal to interference and noise ratio.

$SINR = \frac{P_{signal}}{P_{noise}+P_{interference}}$

Interference can also be created by objects in the environment. Buildings and other obstacles to propagation can block regular transmission, causing any signal to make it behind the building to be greatly attenuated. This is called shadowing. Note that this not only happens to the line-of-sight components of the wave front, but any multi path ray! For this reason, buildings and other obstacles give rise to large-scale fading by creating a diffraction pattern of the signal wave in the shadow of the building.

These components can undergo many types of transformations. Reflection is when a field reaches an object with very large dimensions compared to the wavelength of the field. A wi-fi signal is reflected off of buildings and the ground, creating patterns of de/coherence. Diffraction occurs when a transmitter and receiver are obstructed by a surface, 'bending' the wave around the obstacle. When a field travels across a surface with dimensions that are small compared to its wavelenght and where the number of obstacles per volume is high. Refraction is a result of the field traversing multiple mediums, much like how a pencil appears to 'bend' when placed in a glass of water. For much higher frequencies (starting at 15Ghz), atmospheric absorption is a problem, but for indoor distances and low frequencies, the effects are negligible. [Source Tum]

Log-Normal Shadowing Propagation Loss Model

The next model builds on the Log-Normal shadowing model by including a random variable, $chi$. This law can be expressed as:

$PL_{d_0\rightarrow d}(dB)=PL(d_0)+10n\log_{10}\frac{d}{d_0}+\chi_2$

Where $\chi_2$ is a zero-mean Gaussian distributed random variable. This variable is only used when there is a shadowing effect. Equivalently, $\chi_2=0$ when no shadowing effect is present.

Two Ray Ground Propagation Loss Model

Thus far, we have not needed to think of our signal and other multipath components as being complex vectors. When we start trying to predict the way these multiple paths interact analytically, phase shifting due to refraction, fading, and other multipath effects can be modelled by using a two path tracing technique. The figure below illustrates this model.

Figure 1. - Two Ray Path Loss Model.

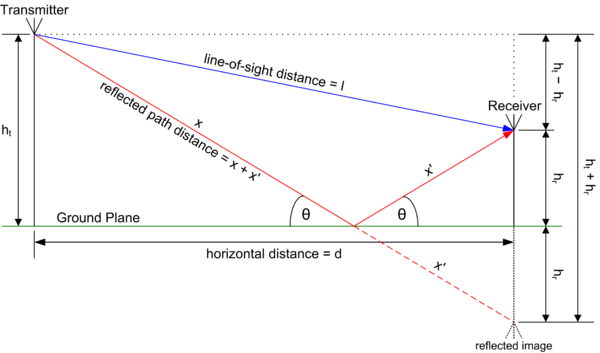
ITU Propagation Loss Model

The next model is a semi-empirical model, based on the same Friis equatoin, with added parameters for noise due to fading between floors in a building.

$PL_{d_0\rightarrow d}(dB)=PL(d_0)+20n\log_{f}+N(\log_{10}(d)+P_f(n)-28$ Where $P_f$(n) is a power loss function due to the number of floors through which the field propagates. In addition, the $\chi$ value of previous models has been set to -28 in the ITU model, taken from standardized urban measurements. Source: ITU.pdf

Motley-Keenan Model

The Motley-Keenan Model follows the same logic.
$PL_{d_0\rightarrow d}(dB)=PL(d_0)+20\log_{10}\frac{d}{d_0}+\sum a_K$
$PL_{LoS}(d)[dB]=20log_{10}\frac{(4πd_0)}{λ}+10_{n_{LoS}}log_{10}(d)+\chi_{\sigma}$
$PL_{NLoS}(d)[dB]=20log_{10}\frac{(4πd_0)}{λ}+10_{n_{NLoS}}log_{10}(d)+\chi_{\sigma}$ $PL_{LoS}(d)[dB]=P_{LoS}*PL_{LoS}(d)[dB]+(1-P_{LoS})*PL_{NLoS}(d)[dB]$

Source: m-k 3

Tata Modified ITU Model

$PL_{T−IPLM}(dB)=20 × log_{10}(f) + N_T × log_{10}(d)+10+\sum_{w=0}^{w=k}+FAF-20$

NT for different number of obstacles

	Channel 1		Channel 7		Channel 11
No. Obstacles	$N_T$	No. Obstacles	$N_T$	No. Obstacles	$N_T$
1	31.1	1	32.9	1	29.3
2	30.1	2	28.5	2	28.4
3	31.8	3	26.7	3	27
4	31.2	4	29.1	4	28
5	31.3	5	27.4	5	28.4

Floor Wise Attenuation Factor (FAF)

Scenario	FAF (dB)
-2 floors	36
-1 floors	21
0 floors	0
+1 floors	21
+2 floors	33
+3 floors	40

Longley-Rice Model:

Frequency
Distance
Antenna Heights
Polarization
Terrain irregularity ($\Delta h$)
Electrical Ground constants
Refractivity
Climate
Siting
Reliability and confidence level

w' (t,ℓ,s) = W0 + yS(s) + δL(s) yL(ℓ) + δT(s) yT(t),
https://www.ntia.doc.gov/files/ntia/publications/ntia_82-100_20121129145031_555510.pdf

## Purely Statistical Models

Rayleigh Fading

$x = cdf(r_{min})\approx \frac{r^2_{min}}{2\sigma^2}$

Rician Fading

Doppler Adjustments

$BER_{Doppler} = \frac{1}{2} \pi^2(v_{max}T_B)^2 $

$BER = K (\frac{S_{\tau}}{T_B})^2$

Machine Learning

Problem

Standard wireless models are great at modelling unbostructed line-of-sight connections. However, they fail to accurately model the network states at peak noise, in complicated urban environments both indoors and outdoors. In addition, these models live entirely in the proprietary world of the IEEE website. Implementing these models in Python would go a long way to modelling the bigger problem. This is the first step. Since some quantities required for these models are unknown, a gridsearch algorithm will be used to optimize these algorithms.

Since these models require different sets of parameters, what features our dataset needs is an open question. The first method will be using a k-random-forest algorithm to see what features are relevant to the signal strength between two nodes.

The next method will take the most useful features and use them to build a linear (or maybe quadratic) regressor that predicts signal to noise ratio between two nodes.

Then, each of these models (the set of 802.11 standard models and my from-scratch regressor) will be compared using a Xi-Square test. Differences between my 'simplified' model and the more complex 802.11 models will be compared and analyzed with respect to the cost of finding the additional features.

Model	Required Features
Friis	Receive Power	Transmit Power	Transmitter Gain	Receiver Gain	distance	frequency

Hypothesis

Machine Learning Tools can signinficantly reduce the cost of measurement.