AboutHap

About HAP: Knots, Links and Proteins

Knots and links can be realized as 3-dimensional pure cubical complexes. For instance, the following commands construct the 10th prime knot on 9 crossings and then display the knot. (Data on prime knots with low crossing number has been taken from the Knot Atlas.)

gap> K:=PureCubicalKnot(9,10);
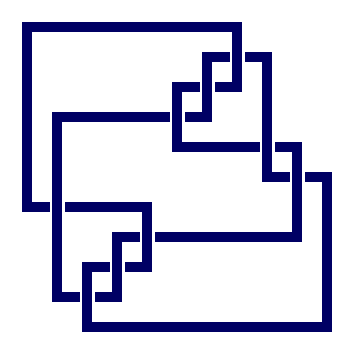
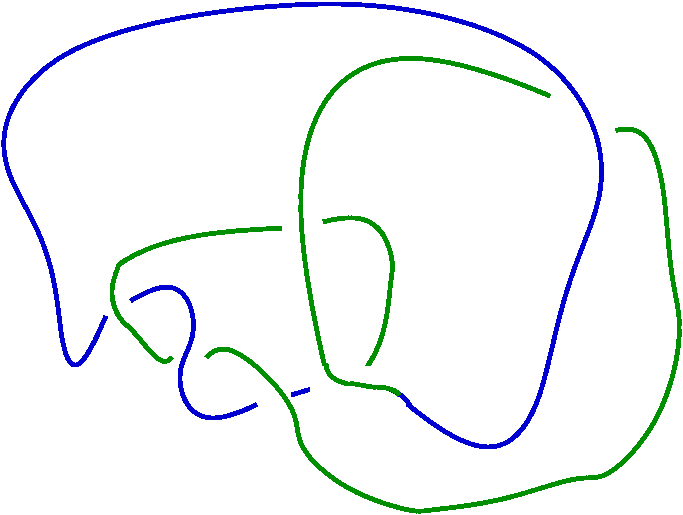
prime knot 10 with 9 crossings

gap> ViewPureCubicalKnot(K);

The following commands display the sum of the 10th and 11th prime knots on 9 crossings.

gap> K:=PureCubicalKnot(9,10);;
gap> L:=PureCubicalKnot(9,11);;
gap> M:=KnotSum(K,L);
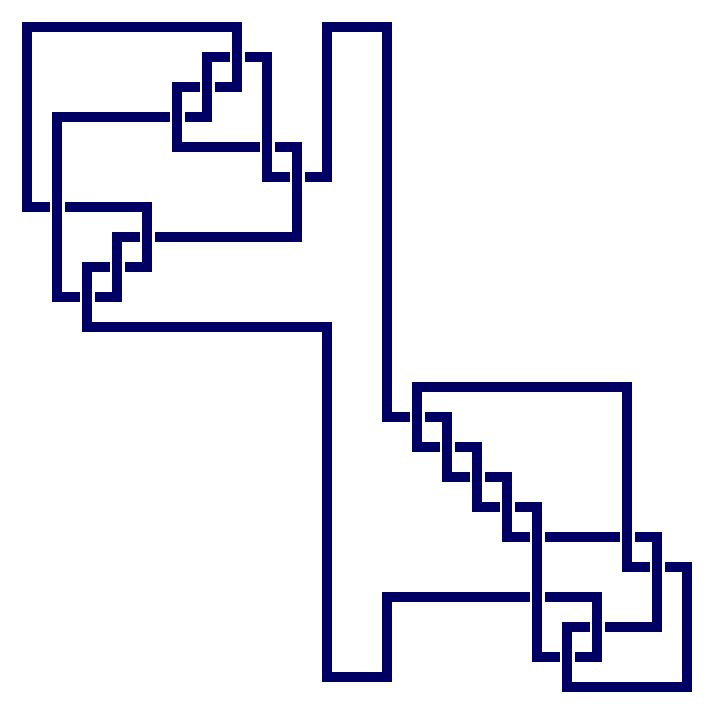
prime knot 10 with 9 crossings + prime knot 11 with 9 crossings

gap> ViewPureCubicalKnot(M);

The following commands compute the Alexander polynomial of the sum of the 10th and 11th knots on 9 crossings. Alexander polynomials are returned with degree 0 coefficient equal to 1.

gap> AlexanderPolynomial(M);
x_1^10-7*x_1^9+77/4*x_1^8-137/4*x_1^7+191/4*x_1^6-215/4*x_1^5+191/4*x_1^4-137/4*x_1^3+77/4*x_1^2-7*x_1+1

Modulo ambient isotopy and mirror image there are 84 prime knots with 9 or fewer crossings. These 84 knots yield 74 distinct Alexander polynomials.

The following commands compute the abelian invariants of the low index subgroups of the knot group G (=fundamental group of knot complement) of the sum of the 10th and 11th knots on 9 crossings. The subgroups H<G of index at most 5 are computed. The abelian invariants are sorted so as to yield an isomorphism invariant of G.

We remark that the abelian invariants of subgroups of index at most 5 in the knot group are sufficient to distinguish between all prime knots on 9 or fewer crossings (up to ambient isotopy and mirror image).

gap> G:=KnotGroup(M);;
gap> Invariants:=List(LowIndexSubgroupsFpGroup(G,5),AbelianInvariants);;
gap> Invariants:=SortedList(Invariants);
[ [ 0 ], [ 0, 0, 0 ], [ 0, 0, 0 ], [ 0, 0, 0 ], [ 0, 0, 0 ],
[ 0, 0, 0, 3, 3, 11, 11 ], [ 0, 0, 2, 3, 5, 7, 7 ], [ 0, 0, 2, 3, 5, 7, 7 ],
[ 0, 0, 2, 3, 5, 7, 7 ], [ 0, 0, 2, 3, 5, 7, 7 ],
[ 0, 0, 3, 3, 3, 7, 7, 11 ], [ 0, 0, 3, 11 ], [ 0, 0, 3, 11 ],
[ 0, 0, 3, 11, 11, 13, 13 ], [ 0, 2, 3, 3, 3, 3, 7, 7, 11 ],
[ 0, 2, 3, 3, 5, 7, 7, 8 ], [ 0, 2, 3, 3, 5, 7, 7, 8 ],
[ 0, 2, 3, 3, 5, 7, 7, 8 ], [ 0, 2, 3, 3, 5, 7, 7, 8 ],
[ 0, 2, 3, 3, 5, 11 ], [ 0, 3, 3, 3, 3, 11, 11 ], [ 0, 3, 3, 11, 11 ],
[ 0, 7, 7, 13, 13 ], [ 0, 59, 59, 79, 79 ] ]

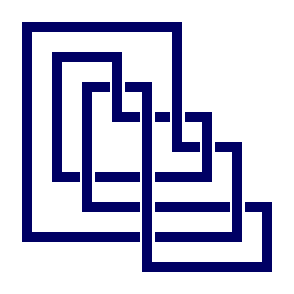
The functions KnotGroup() and PureCubicalKnot() can be applied to links. For instance, the notation [[5, 9],[1, 8],[9, 3],[7, 2],[8, 6],[4, 7],[3, 5],[2, 4],[6, 1]] represents a cubical link with all vertical lines at the front and all horizontal lines at the back. The bottom horizontal line extends from the 5th column to the 9th column. The second to bottom horizontal line extends from the 1st column to the 8th column. And so on until we see that the top horizontal line extends from the 1st column to the 6th column.

gap> C:=[[5, 9],[1, 8],[9, 3],[7, 2],[8, 6],[4, 7],[3, 5],[2, 4],[6, 1]];;
gap> N:=PureCubicalKnot(C);
Pure cubical link.

gap> ViewPureCubicalKnot(N);

gap> G:=KnotGroup(N);
<fp group of size infinity on the generators [ f1, f2, f3 ]>
gap> RelatorsOfFpGroup(G);
[ f1*f2*f1^-1*f3*f2^-1*f3^-1, f2*f3^-1*f1^-1*f2*f3*f2^-1*f1^2*f2^-1*f1^-1 ]

The Protein Data Base contains a wealth of data which can be investigated with respect to knottedness. Information on a particular protein can be downloaded as a pdb file. Each protein consists of one or more chains of amino acids and the file gives Euclidean coordinates of the atoms in amino acids. Each amino acid has a unique "alpha carbon" atom (labelled as "CA" in the pdb file). A simple path can be constructed through the sequence of alpha carbon atoms. By joining the ends of this path one obtains a simple closed curve in Euclidean 3-space. For instance, the pdb file of the T.thermophilus 1V2X protein, which consists of a single chain of amino acids, can be read as a 3-dimensional pure cubical complex (of the homotopy type of a circle) using the following commands.

gap> Kprotein:=ReadPDBfileAsPureCubicalComplex("1V2X.pdb");
Read chain of 190 amino acids containing 1530 atoms.
Pure cubical complex of dimension 3.

This pure cubical complex can be viewed using the following commands.

gap> ViewPureCubicalComplex(ContractedComplex(Kprotein));

The fundamental group of the complement of this protein (whose ends have been joined) can be obtained using the following commands.

gap> C:=ComplementOfPureCubicalComplex(Kprotein);;
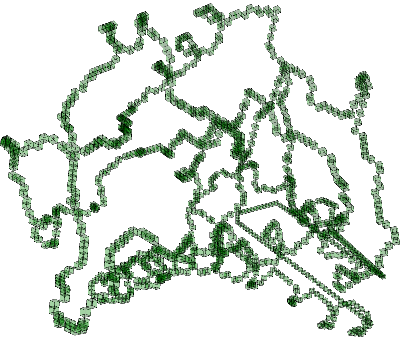
gap> C:=ZigZagContractedPureCubicalComplex(C);;
gap> G:=FundamentalGroup(C);
<fp group of size infinity on the generators [ f1, f2 ]>

gap> RelatorsOfFpGroup(G);
[ f2*f1^-1*f2*f1*f2^-1*f1 ]

The following command shows that this fundamental group, and hence the protein knot, is non-trivial since it has Alexander polynomial equal to that of the trefoil group.

gap> AlexanderPolynomial(G);
x_1^2-x_1+1

The H.sapiens 1XD3 protein contains a more complicated knot, as the following commands show. This pdb file needs to be read at a "resolution" value of 5 or greater in order for the successful representation of it as a pure cubical complex of the homotopy type of a circle..

gap> ViewPDBfile("1XD3.pdb");

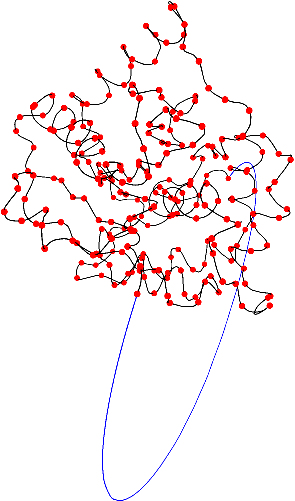
gap> Kprotein2:=ReadPDBfileAsPureCubicalComplex("1XD3.pdb",5);;
Reading chain containing 243 atoms.

gap> C:=ComplementOfPureCubicalComplex(Kprotein2);;
gap> C:=ZigZagContractedPureCubicalComplex(C);;
gap> G:=FundamentaGroup(C);;
#I there are 2 generators and 1 relator of total length 16
gap> AlexanderPolynomial(G);
x_1^2-3/2*x_1+1

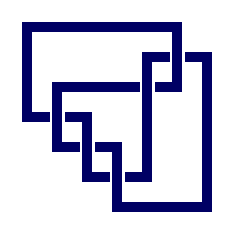
gap> AlexanderPolynomial(PureCubicalKnot(5,2));
x_1^2-3/2*x_1+1

gap> ViewPureCubicalKnot(PureCubicalKnot(5,2));;

We remark that this prime knot on five crossings has unknotting number equal to 1. It is thus possible to convert the knot to the trivial knot by changing one over crossing to an under crossing or vice-versa.

There may be slight errors in the coordinates of atoms in the pdb file for a protein. To test the robustness of the knottedness of a protein we can thicken the protein knot and see if its homotopy type changes. If the homotopy type does change then we can investigate whether the thickening has removed any knottedness.

The following commands show that by thickening the Kprotein2 knot slightly we change its homotopy type to that of a wedge of two circles Sp v Sq, but that a further three thickenings contribute no further change of homotopy type.

gap> Kprotein2:=FramedPureCubicalComplex(Kprotein2);;
gap> Kprotein2:=FramedPureCubicalComplex(Kprotein2);;
gap> Kprotein2:=FramedPureCubicalComplex(Kprotein2);; #This creates some space to perform thickenings

gap> T1:=ThickenedPureCubicalComplex(Kprotein2);;
gap> L:=ContractedComplex(T1);;
gap> Y:=CubicalComplexToRegularCWComplex(L);;
gap> CriticalCellsOfRegularCWComplex(Y);
[ [ 1, 571 ], [ 1, 601 ], [ 0, 6877 ] ]

gap> T2:=ThickenedPureCubicalComplex(T1);;
gap> T3:=ThickenedPureCubicalComplex(T2);;
gap> T4:=ThickenedPureCubicalComplex(T3);;
gap> L:=ContractedComplex(T4);;
gap> Y:=CubicalComplexToRegularCWComplex(L);;
gap> CriticalCellsOfRegularCWComplex(Y);
[ [ 1, 380 ], [ 1, 468 ], [ 0, 9436 ] ]

The following commands show that the complement of the thickened space T3 has the homotopy type of a wedge of two circles and one 2-sphere. In particular, this is quite different to the homotopy type of the complement of the wedge of circles obtained from the unknot by squeezing diagonally opposite points together.

gap> C:=ComplementOfPureCubicalComplex(T3);;
gap> C:=ZigZagContractedPureCubicalComplex(C);;
gap> Y:=CubicalComplexToRegularCWComplex(C);;
gap> CriticalCellsOfRegularCWComplex(Y);
[ [ 2, 68 ], [ 1, 88018 ], [ 1, 113335 ], [ 0, 49422 ] ]

gap> G:=FundamentalGroup(Y);
<fp group of size infinity on the generators [ f1, f2 ]>
gap> RelatorsOfFpGroup(G);
[ ]

The following commands show that the first circle Sp of the wedge T3 is unknotted.

gap> P:=RandomCubeOfPureCubicalComplex(T3);;
gap> P:=ThickenedPureCubicalComplex(P);;
gap> P:=ThickenedPureCubicalComplex(P);;
gap> P:=ThickenedPureCubicalComplex(P);;
gap> P:=ThickenedPureCubicalComplex(P);;
gap> Sp:=PureCubicalComplexDifference(T3,P);;
gap> ContractPureCubicalComplex(Sp);;
gap> Sp:=ThickenedPureCubicalComplex(Sp);; #Makes Sp into a topology manifold again
gap> Cp:=ComplementOfPureCubicalComplex(Sp);;
gap> Cp:=ZigZagContractedPureCubicalComplex(Cp);;
gap> Yp:=CubicalComplexToRegularCWComplex(Cp);;
gap> CriticalCellsOfRegularCWComplex(Yp);
[ [ 1, 14 ], [ 0, 28 ] ]

The following commands show that the second crice Sq of the wedge T3 is again unknotted.

gap> Q:=RandomCubeOfPureCubicalComplex(Sp);;
gap> Q:=ThickenedPureCubicalComplex(Q);;
gap> Q:=ThickenedPureCubicalComplex(Q);;
gap> Q:=ThickenedPureCubicalComplex(Q);;
gap> Q:=ThickenedPureCubicalComplex(Q);;
gap> Sq:=PureCubicalComplexDifference(T3,Q);;
gap> ContractPureCubicalComplex(Sq);;
gap> Sq:=ThickenedPureCubicalComplex(Sq);; #Makes Sq into a topology manifold again
gap> Cq:=ComplementOfPureCubicalComplex(Sq);;
gap> Cq:=ZigZagContractedPureCubicalComplex(Cq);;
gap> Yq:=CubicalComplexToRegularCWComplex(Cq);;
gap> CriticalCellsOfRegularCWComplex(Yq);
[ [ 1, 27 ], [ 0, 19 ] ]

The following commands determine the relative sizes of the two circles Sp and Sq, showing that Sp is about four times longer than Sq.

gap> ContractPureCubicalComplex(Sp);;
gap> Size(Sp);
2839

gap> ContractPureCubicalComplex(Sq);;
gap> Size(Sq);
747

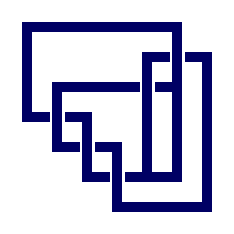
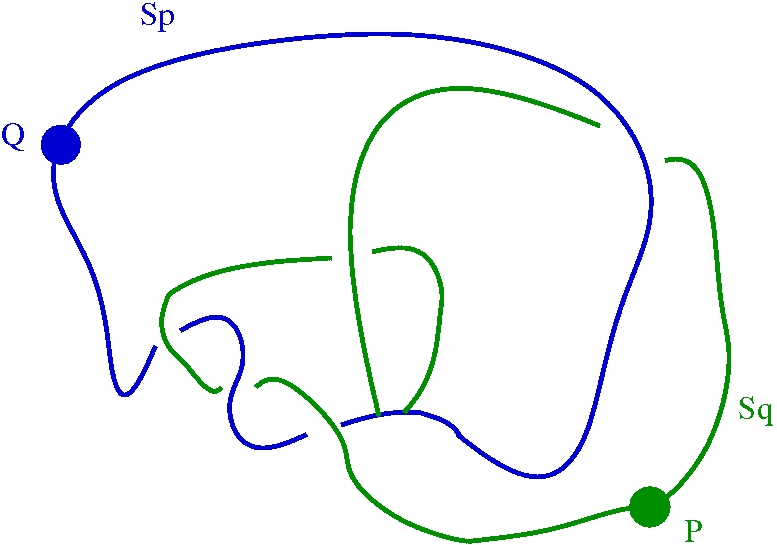
Thus a slight thickening of the protein knot of 1XD3 significantly changes its homotopy type and knottedness. Further commands can be used establish that the thickened protein knot and complement have the same homotopy types as a space such as

and its complement.

However, a further three thickenings of the 1XD3 protein knot contribute no further changes to homotopy type.

In conclusion, the nature of the knot in the protein 1XD3 is very sensetive to the accuracy of the Euclidean coordinates of its alpha carbon atoms given in the pdb file. A slight change in the coordinates of certain atoms can change the ambient isotopy of the knot in the protein to a knot such as the trefoil knot:

but not to the trivial protein knot.

Contents