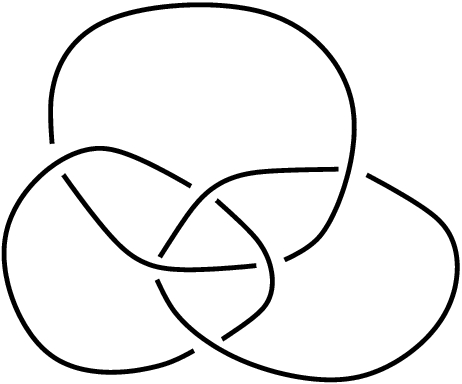
|
As
an
illustration
of HAP's functions for cellular spaces we use them to
obtain a presentation for the fundamental group of the complement of
the
Borromean rings link in Euclidean 3-space. (The method uses no
specialized techniques from knot theory and can be applied to fairly
arbitrary subspaces of Euclidean space.)
|
The
function ReadLinkImageAsPureCubicalComplex("link.eps")
inputs an image file containing a link diagram and tries to output the
corresponding link as a 3-dimensional pure cubical complex. Ideally the
link diagram should have dimensions (line thickness, under-crossing
spaces etc) similar to that of the Borromean rings diagram above. The
function does not always succeed: it applies several checks, and if one
of these checks fails then the function returns "fail".
The following commands succeed in using the above image to realize the
the Borromean rings as
a pure cubical complex with 33654 3-dimensional cubes.
|
gap>
L:=ReadLinkImageAsPureCubicalComplex("borromean-rings.jpg");
Pure cubical complex of dimension 3.
gap> Size(L);
33654
|
The
following commands confirm that L has the correct homology.
|
gap>
Homology(L,0);
[ 0, 0, 0 ]
gap> Homology(L,1);
[ 0, 0, 0 ]
gap> Homology(L,2);
[ ]
|
The
following commands produce a 3-dimensional pure cubical complex C that
is homotopy equivalent to the complement of the Borromean rings in
Euclidean 3-space. The complex C involves 116123 3-dimensional cubes.
|
gap>
C:=ComplementOfPureCubicalComplex(L);
Pure cubical complex of dimension 3.
gap> C:=ZigZagContractedPureCubicalComplex(C);
Pure cubical complex of dimension 3.
gap> Size(C);
116123
|
The
next commands convert C to a regular CW-space Y involving a total of
1447707 cells of dimension 0,1,2 and 3. The CW-structure on Y is
precisely that of the pure cubical complex C.
|
gap>
Y:=CubicalComplexToRegularCWSpace(C);
Regular CW-space of dimension 3
gap> Size(Y);
1447707
|
Next
we
construct
a discrete vector field on Y which has just 9 critical
cells, three in dimension 2, four in dimension 1, and two zero cells.
|
gap>
CriticalCellsOfRegularCWSpace(Y);
[ [ 2, 334 ], [ 2, 115000 ], [ 2, 139630 ], [ 1, 386713 ], [ 1, 404957
],
[ 1, 405056 ], [ 1, 600331 ], [ 0, 164802 ], [ 0, 241782 ] ]
|
Discrete
Morse
Theory
tells us that there exists a CW-space W that is homotopy
equivalent to Y (and C) and that has just three 2-cells, four 1-cells
and two 0-cells. The space W can be used to find a presentation of
the fundamental group of Y and to determine the homology of Y.
The following commands use W to confirm that the link complement Y has
the correct integral homology.
|
gap>
Homology(Y,0);
[ 0 ]
gap> Homology(Y,1);
[ 0, 0, 0 ]
gap> Homology(Y,2);
[ 0, 0, 0 ]
|
The
following commands use W to determine a presentation for the
fundamental group of the link complement Y.
|
gap>
F:=FundamentalGroup(Y);
<fp group on the generators [ f1, f2, f3 ]>
gap> RelatorsOfFpGroup(simplifiedF);
[ f3^-1*f2^-1*f3*f1^-1*f2*f3*f2^-1*f3^-1*f1*f2,
f2^-1*f3^-1*f1*f3*f1^-1*f2*f1*f3^-1*f1^-1*f3 ]
|
Note
that
the
abelianization Fab is free abelian of rank 3.
This is consistent with the isomorphism H1(Y,Z) = H1(F,Z).
|
The
fundamental group F can be used to compute some link invariants. For
instance, we can compute the degree 3 integral homology of its class 2
nilpotent quotient G:=F/[[F,F],F] .
|
gap>
G:=NilpotentQuotient(F,3);;
gap> GroupHomology(G,3);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
|
The
following commands compute the same homological invariant for the
following link
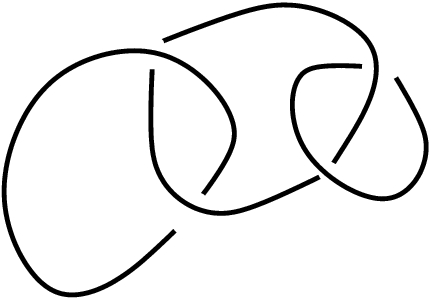
and, as the value of the invariant is different in this case, the
computations prove that
the Borromean rings are not ambient isotopic to this second link.
|
gap>
L:=ReadLinkImageAsPureCubicalComplex("link.jpg");;
gap> C:=ComplementOfPureCubicalComplex(L);;
gap> C:=ZigZagContractedPureCubicalComplex(C);;
gap> Y:=CubicalComplexToRegularCWSpace(C);;
gap> F:=FundamentalGroup(Y);
gap> G:=NilpotentQuotient(F,3);;
gap> GroupHomology(G,3);
[ 0, 0, 0, 0, 0, 0 ]
|
|