
This chapter describes functions to be used in connection with the numericalsgps package. We found it particularly usefull to gain intuition that led to the obtention of the results stated in [DGSRP16].
‣ TikzCodeForNumericalSemigroup( arg ) | ( function ) |
The arguments (at most 4) are:
a numerical semigroup
(optional) a list whose elements are either
lists of integers or
one of the strings "pseudo_frobenius", "small_elements", "min_generators", "frobenius_number", "conductor", "special_gaps", "fundamental_gaps" (the default: used when no list is present) or
a record whose fields are
func -- a function name
(optional) argument -- an argument (that may be a function name also)
(optional) a positive integer -- if it is bigger than the conductor or biggest minimal generator, it indicates the number of cells - 1 to be drawn and these are drawn in a single line; otherwise, it indicates the maximum number of cells per line.
gap> ns1 := NumericalSemigroup(3,5);; gap> TikzCodeForNumericalSemigroup(ns1,[[3,4],"pseudo_frobenius"],20); "%tikz\n\\begin{tikzpicture}[every node/.style={draw,scale=1pt,\nminimum width\ =20pt,inner sep=3pt,\nline width=0pt,draw=black}]\n\\matrix[row sep=2pt,column\ sep=2pt]\n{\\node[]{0};&\n\\node[]{1};&\n\\node[]{2};&\n\\node[fill=red]{3};&\ \n\\node[fill=red]{4};&\n\\node[]{5};&\n\\node[]{6};&\n\\node[fill=green]{7};&\ \n\\node[]{8};&\n\\node[]{9};&\n\\node[]{10};&\n\\node[]{11};&\n\\node[]{12};&\ \n\\node[]{13};&\n\\node[]{14};&\n\\node[]{15};&\n\\node[]{16};&\n\\node[]{17}\ ;&\n\\node[]{18};&\n\\node[]{19};&\n\\node[]{20};\\\\\n};\n\\end{tikzpicture}\ \n"
gap> IP_Splash(TikzCodeForNumericalSemigroup(NumericalSemigroup(7,13,19,23), > [[3,4],"small_elements","fundamental_gaps"],20),rec(viewer := "evince"));

‣ SetOfNumericalSemigroups( arg ) | ( function ) |
This function is used to produce lists of numerical semigroups with a fixed genus or Frobenius number. They are filtered and ordered according to some criteria.
The argument is a record of options:
set -- a record whose possible fields are genus or frobenius
(optional) filter -- a record whose possible fields are genus, type and/or multiplicity and/or frobenius and/or embedding_dimension
(optional) order -- ("genus", "type", "multiplicity", "frobenius", "embedding_dimension")
gap> SetOfNumericalSemigroups(rec(set:=rec(genus:=6),filter:=rec(type:= 2), > order:="multiplicity")); [ <Numerical semigroup with 3 generators>, <Numerical semigroup with 3 generators>, <Numerical semigroup with 4 generators>, <Numerical semigroup with 5 generators>, <Numerical semigroup with 5 generators>, <Numerical semigroup with 6 generators> ] gap> SetOfNumericalSemigroups(rec(set:=rec(genus:=6),filter:=rec(type:= 2), > order:="frobenius")); [ <Numerical semigroup with 3 generators>, <Numerical semigroup with 5 generators>, <Numerical semigroup with 5 generators>, <Numerical semigroup with 3 generators>, <Numerical semigroup with 4 generators>, <Numerical semigroup with 6 generators> ] gap> List(last,MinimalGeneratingSystem); [ [ 3, 10, 11 ], [ 5, 6, 7 ], [ 5, 6, 8 ], [ 3, 8, 13 ], [ 4, 7, 9 ], [ 6, 7, 8, 9, 11 ] ]
‣ DrawSetOfNumericalSemigroups( arg ) | ( function ) |
Produces a single image from the images of a set of numerical semigroups.
The arguments (at most 3) are:
a list of numerical semigroups (given as a list or each given as argument)
(optional) an integer that (when present) determines the length of each line
(optional) a record whose fields are
(optional) splash -- which (when present) consists of a record of options for the Viz Splash function
(optional) highlights: a list to be passed to the function that produces the tikz code for each individual semigroup (whose aim is to say which elements are to be highlighted)
gap> ns1 := NumericalSemigroup(3,5);; gap> ns2 := NumericalSemigroup(5,7,11);; gap> DrawSetOfNumericalSemigroups(ns1,rec(splash:= > rec(viewer := "evince"),highlights := > ["pseudo_frobenius","small_elements","min_generators"])); gap> DrawSetOfNumericalSemigroups(ns1,ns2,rec(splash:= > rec(viewer := "evince"),highlights := > ["pseudo_frobenius","small_elements","min_generators"])); gap> DrawSetOfNumericalSemigroups([ns1,ns2],rec(splash:= > rec(viewer := "evince"),highlights := > ["small_elements","min_generators"]));



gap> frob := 15;; gap> tipo := 2;; gap> set := SetOfNumericalSemigroups(rec(set := rec(frobenius := frob), > filter := rec(type:= tipo),order := "embedding_dimension"));; gap> DrawSetOfNumericalSemigroups(set,rec(splash:= rec(viewer := "evince"), > highlights := ["small_elements","min_generators", > rec(func:= "ForcedIntegersForPseudoFrobenius", > argument := "PseudoFrobeniusOfNumericalSemigroup")]));
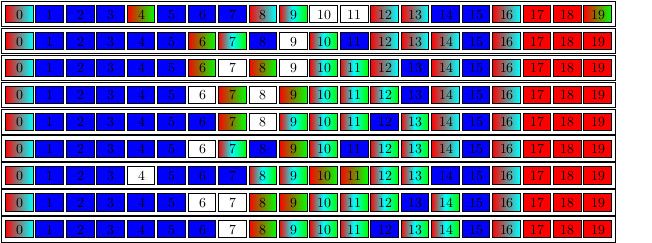
gap> ns := NumericalSemigroup(4,9,19);; gap> SmallElements(ns); [ 0, 4, 8, 9, 12, 13, 16 ] gap> MinimalGeneratingSystem(ns); [ 4, 9, 19 ] gap> ForcedIntegersForPseudoFrobenius(PseudoFrobeniusOfNumericalSemigroup(ns)); [ [ 1, 2, 3, 5, 6, 7, 14, 15 ], [ 0, 8, 9, 12, 13, 16 ] ]
generated by GAPDoc2HTML