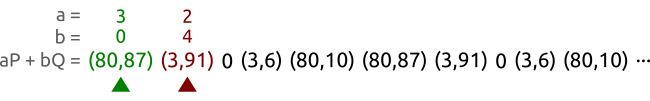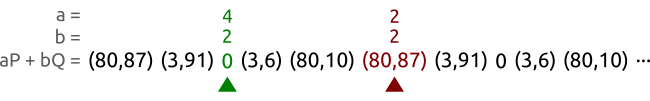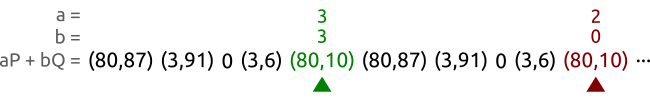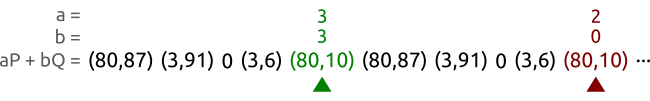README.md

Pollard Rho Algorithm for solving ECDLP

Prerequisites:

1. Elliptic Curve Discrete Logarithm Problem

Pollard Rho Algorithm for solving ECDLP will give a unique solution in cases where order of the group, over which the DLP is defined, is a prime number. Otherwise, it can give multiple solutions.

To find any two pairs & such that

Once we have these pairs, we can write:

Let base point P have order = n. Then we can write: , provided GCD((B-b), n) == 1

But the problem is, how do we calculate (a, b) and (B, b)?

Brute Forcing such pairs will be of the order which is even larger than the brute force algorithm for solving ECDLP: .

We can use Floyd's Cycle Finding Algorithm to reduce the complexity! Have a look at how the Cycle Finding algorithm can be efficiently used to solve ECDLP:

Source: https://andrea.corbellini.name/2015/06/08/elliptic-curve-cryptography-breaking-security-and-a-comparison-with-rsa/

Basically, the algorithm is

1. Initially select any integral values for the two pairs ,

2. Keep calculating and , until

   • Check if ,

     • If true, then start again from (1)

     • If false, then return as x

How to calculate , ,

Function f(x):

                      /----------------------------------------------------------|
                     /    X_i + Q = a_i*P       + (b_i + 1)*Q   , X_i[0] in S_1  |
func_f() ~ f(X_i) = /     2*X_i   = (2*a_i)*P   + (2*b_i)*Q     , X_i[0] in S_2  |
                    \     X_i + P = (a_i + 1)*P + b_i*Q         , X_i[0] in S_3  |
                     \-----------------------------------------------------------|

Note: Since is a point and not an integer, we simply partition using x-coordinate of

We can conclude from the above formula that the value of depends upon the set (S_1, S_2, S_3) to which belongs.

Now, we need to calculate values of and . Both of them will also depend upon the set(S_1, S_2, S_3) to which X_i belongs.

Function g(x) and h(x):

                       /--------------------------------|
                      /    a_i         , X_i[0] in S_1  |
func_g() ~ a_(i+1) = /     2*a_i       , X_i[0] in S_2  |
                     \     (a_i + 1)   , X_i[0] in S_3  |
                      \---------------------------------|

                       /--------------------------------|
                      /    (b_i + 1)   , X_i[0] in S_1  |
func_h() ~ b_(i+1) = /     2*b_i       , X_i[0] in S_2  |
                     \     b_i         , X_i[0] in S_3  |
                      \---------------------------------|

I implemented the algorithm in python/sage (with appropriate comments/explanation) here: pollardrho.py

References

1. Andrea Corbellini- Pollard's Rho

2. Section 3.6.3 of chapter-3 from Handbook of Applied Cryptography