Path: blob/master/activities/first_notebook.ipynb
1306 views
Kernel: Unknown Kernel
Lissajous curves
Lissajous curves are a family of parametric two-dimensional curves normally obtained when solving multi-harmonic systems, like a mass-spring systems with two springs in each axis (x and y) or some circuit systems. The figures are described with the following equations:
where and are the amplitudes along each axis, and the angular frequencies and the relative phase.
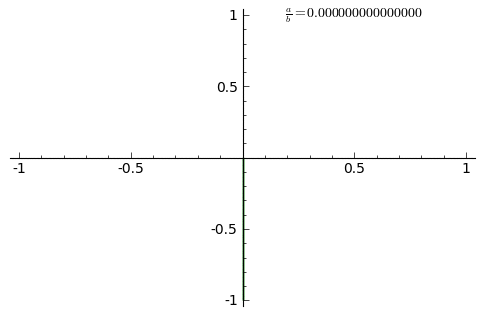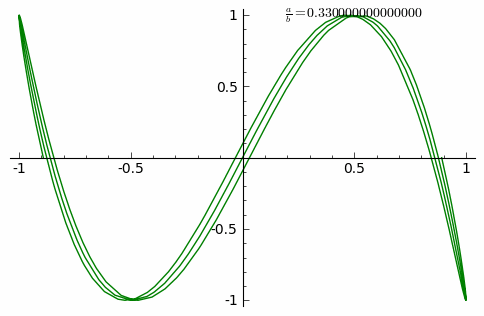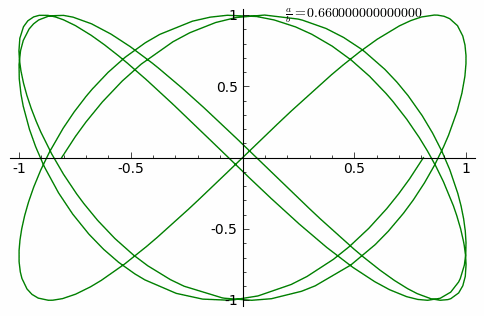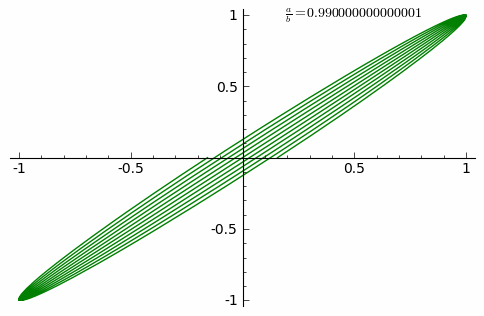
In [1]:
Out[1]:
Welcome to pylab, a matplotlib-based Python environment [backend: module://IPython.zmq.pylab.backend_inline].
For more information, type 'help(pylab)'.
Plotting some curves
In [3]:
In [36]:
Out[36]: