gauss-jordan.ipynb

Kernel: Unknown Kernel

Task 8

This homework is an activity intended to apply the methods to solve systems of equations given in class. The objective is to solve a simple circuit problem by using a modification of the Gaussian Elimination method, called Gauss-Jordan method.

Due to: Feb 22

---

Gauss-Jordan Method

As covered during class, Gaussian Elimination is a procedure where any augmented matrix (associated to a soluble problem with $n$ equations and $n$ unknows) is converted to an equivalent upper diagonal system:

ParseError: KaTeX parse error: Undefined control sequence: \matrix at position 8: \left[ \̲m̲a̲t̲r̲i̲x̲{ a_{11} & a_{1…

At this point, the solution $\{x_i\}_{i=1}^n$ is easily obtained through the formulas:

$$x_n = \hat b_n$$$$x_{n-1} = \frac{\hat b_{n-1} + a_{(n-1)n}x_n}{a_{(n-1)(n-1)}}$$$$\vdots$$$$x_i = \frac{\hat b_i - \sum_{j=i+1}^n a_{ij}x_j}{a_{ii}}\ \ \ \ \mbox{for}\ \ \ i=n-1, n-2, \cdots, 1$$

However, a more direct way to find the solution is to reduce the matrix even more, such that the next diagonal form of the matrix is obtained:

ParseError: KaTeX parse error: Undefined control sequence: \matrix at position 8: \left[ \̲m̲a̲t̲r̲i̲x̲{ a_{11} & 0 & …

and the solution is just given by:

$$x_i = \frac{\hat b_{i}}{a_{ii}}\ \ \ \ \mbox{for}\ \ \ i=n-1, n-2, \cdots, 1$$

1. Starting from an upper diagonal and augmented matrix, describe the necessary steps to obtain an equivalent matrix in a complete diagonal form (Gauss-Jordan method).

2. Using the next routine Gaussian_Elimination, creates a new routine called Gauss-Jordan that computes the diagonal form of any given matrix along with the solution vector $\{x_i\}_{i=1}^n$. Use algorithm of the previous item.

#Lambda function
def row_lamb( i, lamb, A ):
    B = np.copy(A)
    B[i] = lamb*B[i]
    return B

#Combination function
def row_comb( i, j, lamb, A ):
    B = np.copy(A)
    B[i] = lamb*B[j] + B[i]
    return B

#Swap function
def row_swap( i, j, A ):
    B = np.copy(A)
    B[[i,j]] = B[[j,i]]
    return B

#Gaussian Elimination
def Gaussian_Elimination( A0 ):
    #Making local copy of matrix
    A = np.copy(A0)
    #Detecting size of matrix
    n = len(A)
    
    #Sweeping all the columns in order to eliminate coefficients of the i-th variable
    for i in xrange( 0, 4 ):
        
        #Sweeping all the rows for the i-th column in order to find the first non-zero coefficient
        for j in xrange( i, n ):
            if A[i,j] != 0:
                #Normalization coefficient
                Norm = 1.0*A[i,j]
                break
                
        #Applying swap operation to put the non-zero coefficient in the i-th row
        A = row_swap( i, j, A )
        
        #Eliminating the coefficient associated to the i-th variable
        for j in xrange( i+1, n ):
            A = row_comb( j, i, -A[j,i]/Norm, A )
            
    #Normalizing n-th variable
    A = row_lamb( n-1, 1.0/A[n-1,n-1], A )
    
    #Finding solution
    x = np.zeros( n )
    x[n-1] = A[n-1,n]
    for i in xrange( n-1, -1, -1 ):
        x[i] = ( A[i,n] - sum(A[i,i+1:n]*x[i+1:n]) )/A[i,i]
    
    #Upper diagonal matrix and solutions x
    return A, x

Kirchhoff's Law of Circuits

Using Kirchhoff's law, it is possible to solve the currents $i_1,\cdots, i_5$.

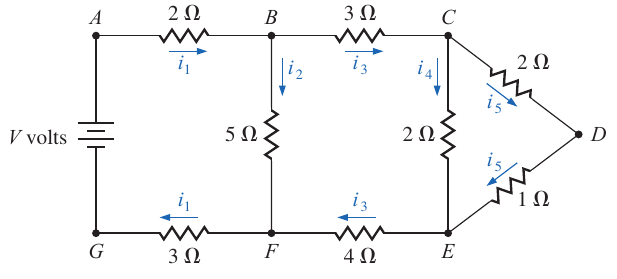
The next system of equations is obtained:

$$5i_1+5i_2 = V$$$$i_3-i_4-i_5 = 0$$$$2i_4-3i_5 = 0$$$$i_1-i_2-i_3 = 0$$$$5i_2-7i_3-2i_4 = 0$$

3. Rewrite this problem using matrix notation. Construct the augmented matrix and solve the problem using the previous routine Gauss-Jordan.

---