Path: blob/master/material/one-variable-equations-fixed-point.ipynb
934 views
Bibliography
[1] Kiusalaas, Numerical Methods in Engineering with Python
[2] Jensen, Computational_Physics. Companion repos: https://github.com/mhjensen Web page
[3] E. Ayres, Computational Physics With Python
Fixed-point Iteration
Although in many cases the use of Bisection is more than enough, there are some pathological situations where the use of more advanced methods is required. One of the advantages featured by this method is one does not have to give an interval where the solution is within, instead, from a seed the algorithm will converge towards the required solution.
Steps FP
Take your function and rewrite it like
In this way, find the root of is equivalent to find the value when This is called the fixed-point of . Note that is just and straight line of slope one and zero intercept. Therefore, the fixed points corresponds to the points where crosses that straight line.
Give a guest to the solution (root of ). This value would be the seed , and correspond to the point:
Check the distance to the straight line by goint to the point:
Go to the point on the straight line: →
The next guest to the solution will be given by → .
Compare with : If the stop condition is not satisfied, then repeat step 2 but now with .
The End!
Example: Find the roots of the next function:
We define
Step 1:
Step 2:
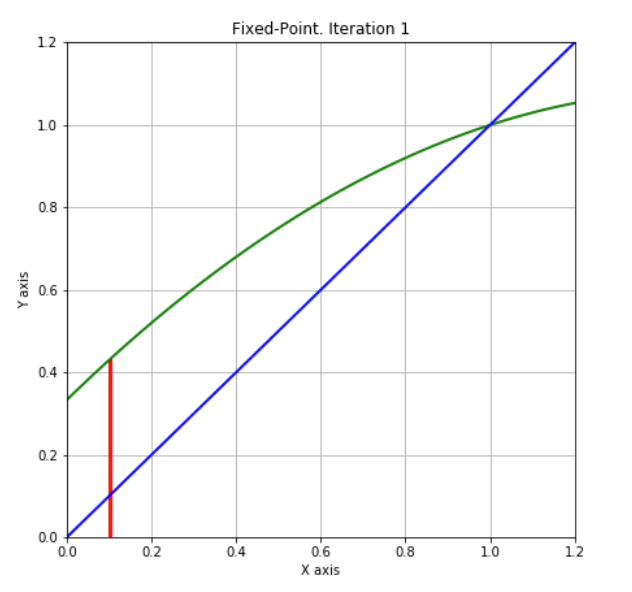
Step 3:
Step 4: Suggest a solution:
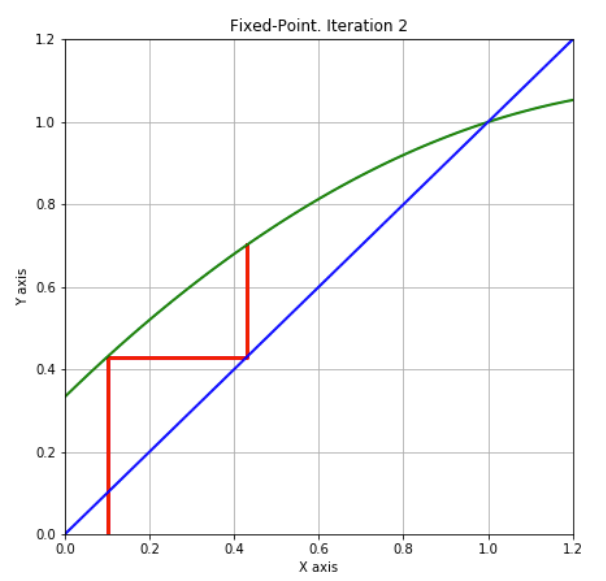
Step 5: Since is still quite differente from we need to continue with another iteration
Implementation of algorithm
Find the roots of the next functions:
using Fixed-Point iteration.
Ejemplo 3:
g(x)=x-f(x)=x_0 g(x_0)=x_0-f(x_0)=x_0
Stop conditions FP
The stop conditions are the same than Bisection:
A fixed distance between the last two steps (absolute convergence):
A fixed relative distance between the last two steps (relative convergence):
Function tolerance:
Computational stop:
If , stop!
Activity: Use the optimize.fixed_point to find the root of f2(x)
Example 4
There is a type of functions whose roots coincides with a local or global minima or maxima. This condition implies the function does not cross the x-axis at the root and the problem cannot be solved by using Bisection as the criterion of different signs cannot be satisfied. Fixed-point iteration is a more feasible alternative when solving these problems.
As an example, here we shall solve the roots of the function
For this, we plot the function first:
It is clear there are three root within the plotted interval, i.e. , and . Using bisection for the first and third roots we obtain:
However, when applying bisection to the middle root, we obtain:
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-33-76a08fa07ea3> in <module>
----> 1 print( "Root x_0", optimize.bisect( f, a=-0.5, b=0.5) )
/usr/local/lib/python3.7/dist-packages/scipy/optimize/zeros.py in bisect(f, a, b, args, xtol, rtol, maxiter, full_output, disp)
547 if rtol < _rtol:
548 raise ValueError("rtol too small (%g < %g)" % (rtol, _rtol))
--> 549 r = _zeros._bisect(f, a, b, xtol, rtol, maxiter, args, full_output, disp)
550 return results_c(full_output, r)
551
ValueError: f(a) and f(b) must have different signs
Now, applying Fixed-point iteration:
Activity: Comprobar con scipy y fixed_point
ACTIVITY FP
When a new planet is discovered, there are different methods to estimate its physical properties. Many times is only possible to estimate either the planet mass or the planet radius and the other property has to be predicted through computer modelling.
If one has the planet mass, a very rough way to estimate its radius is to assume certain composition (mean density) and a homogeneous distribution (a very bad assumption!). For example, for the planet Gliese 832c with a mass , if we assume an earth-like composition, i.e. , we obtain:
That would be the planet radius if the composition where exactly equal to earth's.
A more realistic approach is assuming an internal one-layer density profile like:
where is the density at planet centre and is a characteristic lenght depending on the composition. From numerical models of planet interiors, the estimated parameters for a planet of are are approximately and .
Integrating over the planet volume, we obtain the total mass as
This is a function of the mass in terms of the planet radius.
Solving the equation it would be possible to find a more realistic planet radius. However when using numerical models, it is not possible to approach the solution from the left side as a negative mass makes no sense.
Newton-Raphson Method
Although Fixed-point iteration is an efficient algorithm as compared with Bisection, the Newton-Raphson method is an acceletared convergent scheme where the roots of a function are easily found with just a few iterations.
Derivation NM
Although this method can be presented from an algorithmic point of view, the mathematical deduction is very useful as it allows us to understand the essence of the approximation as well as estimating easily the convergence errors.
Let be a continuous and differentiable function defined within an interval (i.e. ), and is a root of the function such that . If we give an initial an enough close guess to this root, such that , where is adequately small, we can expand the function by using a second order taylor serie, yielding:
but as and is an even smaller quantity, we can readily neglect from second order terms, obtaining
If we repeat this process but now using as our guess to the root instead of we shall obtain:
and so...
where each new iteration is a better approximation to the real root.
Steps NM
Take your function and derive it, .
Give a guest to the solution (root of ). This value would be the seed .
The next guest to the solution will be given by
If the stop condition is not satisfied, then repeat step 3.
The End!
Example 5
Find one root of the function:
with derivative
using the Newton-Raphson method.
Stop conditions NM
The stop conditions are the same than Bisection and Fixed-point iteration:
A fixed distance between the last two steps (absolute convergence):
A fixed relative distance between the last two steps (relative convergence):
Function tolerance:
Computational stop:
If , stop!
Convergence NM
It is possible to demonstrate by means of the previous derivation procedure, that the convergence of the Newton-Raphson method is quadratic, i.e., if is the exact root and is the -th iteration, then
for a fixed ans positive constant .
This implies, if the initial guess is good enough such that |p_0-p| is small, the convergence is achieved very fast as each iteration improves the precision twice in the order of magnitude, e.g., if , , , and so.
ACTIVITY
In an IPython notebook, copy the latter routine NewtonRaphson and the Bisection routine provided in this notebook (and if you have it already, the Fixed-point iteration routine as well) and find the root of the next function using all the methods.
Plot in the same figure the convergence of each method as a function of the number of iterations.
See the Summary section at the end for the implementation in Scipy
Secant Method
The Newton-Raphson method is highly efficient as the convergence is accelerated, however there is a weakness with it: one needs to know the derivative of the function beforehand. This aspect may be complicated when dealing with numerical functions or even very complicated analytical functions. Numerical methods to derive the input function can be applied, but this extra procedure may involve an extra computing time that compensates the time spent by using other methods like Bisection.
Derivation SM
Retaking the iterative expression obtained from the Newton-Raphson method:
or, changing
The derivative can be approximated as
As we know, the convergence of the NR method is quadratic, so should be close enough to such that one can assume and the previous term is:
or, changing
The final expression for the -th iteration of the root is then:
In this consists the Secant method, what is just an approximation to the Newton-Raphson method, but without the derivative term.
Steps SM
Give the input function .
Give two guests to the solution (root of ). These values would be the seeds , .
The next guest to the solution will be given by
If the stop condition is not satisfied, then repeat step 3.
The End!
See the Summary section at the end for the implementation in Scipy
ACTIVITY
In an IPython notebook and based on the routine NewtonRaphson, write your own routine SecantMethod that performs the previous steps for the Secant Method. Test your code with the function :
ACTIVITY
It is known that light rays are deflected when they pass near by a gravitational field and that this deviation is proportional to the body mass which the light is interacting with and inversely proportional to the passing distance. Since it is common finding very massive structures in the universe and the measures that are done to study it involve photons, it makes sense to study what happens to a light source image when the rays get close to a grumpy object like a dark matter halo.
In order to study the light deflection in these cases, it will be used the simplest model, gravitational lens theory, where the len is a very massive object. A sketch of a typical system is shown in the figure below. The source plane is the light source or image that is going to be affected, is the distance from a image point to the line of sight and the subtended angle by the point. The lens plane corresponds to the mass that affects the light coming from the source, is the new image point distance to the line of sight, is the subtended angle by the new point position. Then, is the deflection angle.
Since from observations is known, the problem to be solved per pixel usually is
but also depends on besides the len halo properties. This would allow construct the real image from the distorted and magnified one.

This equation can also be written in terms of distances
The solution to the lens equation is easier to get if it is assumed that the len is axially symmetric. In this case, the deflection angle takes the next form
The quantity is the surface mass density, i.e., the len's mass enclosed inside circle per area unit. It is important to notice that the direction of is the same as and consequently .
The problem to be solved is the next: Given the positions of a square find the image distorsion due to gravitational lensing, i.e., find the root of \xi in the trascendal equation it satisfies. Use the routines given below and all of the data for the len and image that is going to be distorted.
Summary
optimize.bisect
optimize.fixed_point
optimize.newton
In scipy.optimize the newton method contains both the secant and Newton-Raphson algorithms. The las one is used when the derivative of the function is used explicitly
Brent's method.
Find a root of a function in a bracketing interval using Brent's method.
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-62-2741c04b08c2> in <module>
----> 1 brentq(f,-0.5,0.5)
/usr/local/lib/python3.7/dist-packages/scipy/optimize/zeros.py in brentq(f, a, b, args, xtol, rtol, maxiter, full_output, disp)
774 if rtol < _rtol:
775 raise ValueError("rtol too small (%g < %g)" % (rtol, _rtol))
--> 776 r = _zeros._brentq(f, a, b, xtol, rtol, maxiter, args, full_output, disp)
777 return results_c(full_output, r)
778
ValueError: f(a) and f(b) must have different signs