sngp.ipynb

Kernel: Python 3

Copyright 2021 The TensorFlow Authors.

#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

Aprendizaje profundo consciente de la incertidumbre con SNGP

Ver en TensorFlow.org

Ejecutar en Google Colab

Ver en GitHub

Descargar bloc de notas

En las aplicaciones de IA cuya seguridad es crítica, como la toma de decisiones médicas y la conducción autónoma, o en las que los datos intrínsecamente tienen ruido (por ejemplo, comprensión del lenguaje natural), es importante que un clasificador profundo cuantifique de forma fiable su incertidumbre. El clasificador profundo debe ser capaz de ser consciente de sus propias limitaciones y de cuándo debe ceder el control a los expertos humanos. Este tutorial muestra cómo mejorar la capacidad de un clasificador profundo para cuantificar la incertidumbre utilizando una técnica llamada Proceso neural gaussiano espectral-normalizado (SNGP{.externo}).

La idea central de SNGP es mejorar la conciencia de la distancia de un clasificador profundo aplicando modificaciones sencillas a la red. La conciencia de la distancia de un modelo es una medida de cómo su probabilidad predictiva refleja la distancia entre el ejemplo de prueba y los datos de entrenamiento. Se trata de una propiedad deseable que es común en los modelos probabilísticos estándares (por ejemplo, el proceso Gaussiano{.externo} con núcleos RBF), pero de la que carecen los modelos con redes neuronales profundas. SNGP ofrece una forma sencilla de inyectar este comportamiento de proceso gaussiano en un clasificador profundo manteniendo su precisión predictiva.

Este tutorial implementa un modelo SNGP basado en una red residual profunda (ResNet) sobre el conjunto de datos dos lunas de Scikit-learn{.externo}, y compara su superficie de incertidumbre con la de otros dos enfoques de incertidumbre populares: Abandono de Monte Carlo{.externo} y Ensamble profundo{.externo}.

Este tutorial ejemplifica el modelo SNGP en un conjunto de datos 2D de juguete. Para ver un ejemplo de cómo aplicar SNGP a una tarea de comprensión del lenguaje natural del mundo real usando una base BERT, consulte el tutorial SNGP-BERT. Para ver implementaciones de alta calidad de un modelo SNGP (y de muchos otros métodos de incertidumbre) en una amplia variedad de conjuntos de datos de referencia (como CIFAR-100, ImageNet, Detección de toxicidad en rompecabezas, etc.), consulte la Base de referencia de incertidumbre{.externo}.

Acerca de SNGP

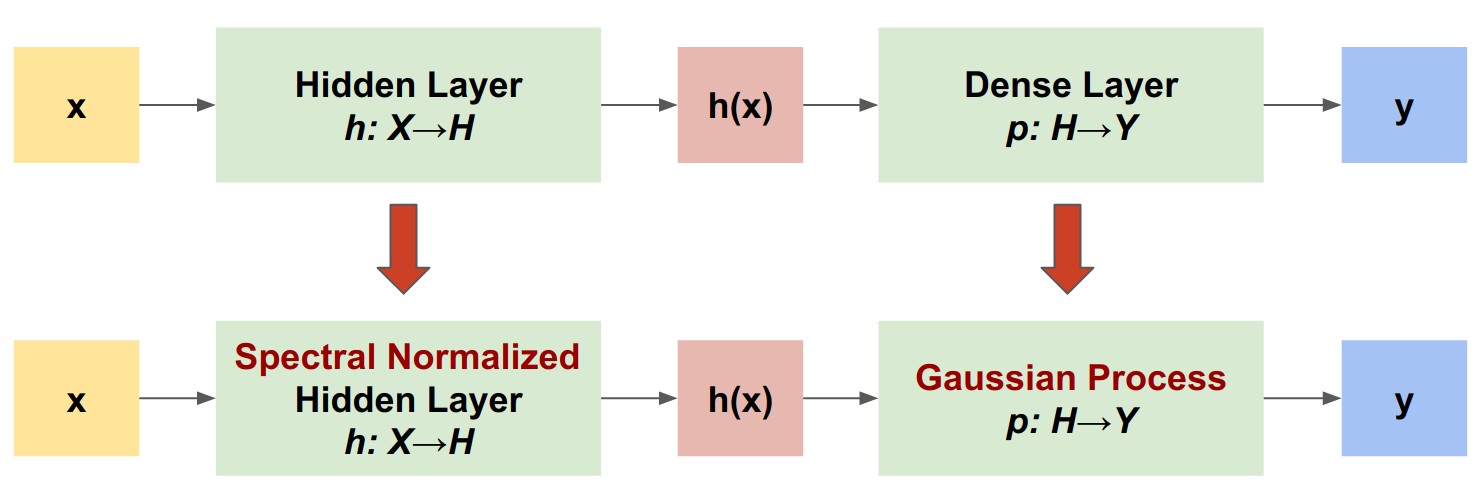
SNGP es un enfoque sencillo para mejorar la calidad de la incertidumbre de un clasificador profundo manteniendo un nivel similar de precisión y latencia. Dada una red residual profunda, SNGP realiza dos cambios sencillos en el modelo:

• Aplica la normalización espectral a las capas residuales ocultas.

• Reemplaza la capa de salida densa por una capa de proceso gaussiano.

En comparación con otros enfoques de incertidumbre (como el abandono de Monte Carlo o el Ensamble profundo), el SNGP presenta varias ventajas:

• Sirve para una amplia gama de arquitecturas basadas en residuos de última generación (por ejemplo, (Wide) ResNet, DenseNet o BERT).

• Se trata de un método de modelo único (no se basa en el promedio de ensambles). Por lo tanto, SNGP tiene un nivel de latencia similar al de una única red determinista, y puede escalarse fácilmente a grandes conjuntos de datos como ImageNet{.externo} y Clasificación de comentarios tóxicos de rompecabezas{.externo}.

• Tiene un fuerte rendimiento de detección fuera del dominio debido a la propiedad conciencia de la distancia.

Los inconvenientes de este método son:

• La incertidumbre predictiva del SNGP se calcula usando la aproximación de Laplace{.externo}. Por lo tanto, teóricamente, la incertidumbre posterior de SNGP es diferente de la de un proceso gaussiano exacto.

• El entrenamiento SNGP necesita un paso de restablecimiento de la covarianza al comienzo de una nueva época. Esto puede añadir una pequeña cantidad de complejidad adicional a un proceso de entrenamiento. Este tutorial muestra una forma sencilla de implementarlo usando retrollamadas de Keras.

Preparación

!pip install -U -q --use-deprecated=legacy-resolver tf-models-official tensorflow

# refresh pkg_resources so it takes the changes into account.
import pkg_resources
import importlib
importlib.reload(pkg_resources)

import matplotlib.pyplot as plt
import matplotlib.colors as colors

import sklearn.datasets

import numpy as np
import tensorflow as tf

import official.nlp.modeling.layers as nlp_layers

Defina macros de visualización

plt.rcParams['figure.dpi'] = 140

DEFAULT_X_RANGE = (-3.5, 3.5)
DEFAULT_Y_RANGE = (-2.5, 2.5)
DEFAULT_CMAP = colors.ListedColormap(["#377eb8", "#ff7f00"])
DEFAULT_NORM = colors.Normalize(vmin=0, vmax=1,)
DEFAULT_N_GRID = 100

El conjunto de datos de dos lunas

Cree los conjuntos de datos de entrenamiento y evaluación a partir del conjunto de datos scikit-learn dos lunas{.externo}.

def make_training_data(sample_size=500):
  """Create two moon training dataset."""
  train_examples, train_labels = sklearn.datasets.make_moons(
      n_samples=2 * sample_size, noise=0.1)

  # Adjust data position slightly.
  train_examples[train_labels == 0] += [-0.1, 0.2]
  train_examples[train_labels == 1] += [0.1, -0.2]

  return train_examples, train_labels

Evalúe el comportamiento predictivo del modelo en todo el espacio de entrada 2D.

def make_testing_data(x_range=DEFAULT_X_RANGE, y_range=DEFAULT_Y_RANGE, n_grid=DEFAULT_N_GRID):
  """Create a mesh grid in 2D space."""
  # testing data (mesh grid over data space)
  x = np.linspace(x_range[0], x_range[1], n_grid)
  y = np.linspace(y_range[0], y_range[1], n_grid)
  xv, yv = np.meshgrid(x, y)
  return np.stack([xv.flatten(), yv.flatten()], axis=-1)

Para evaluar la incertidumbre del modelo, añada un conjunto de datos fuera del dominio (OOD) que pertenezca a una tercera clase. El modelo nunca observa estos ejemplos OOD durante el entrenamiento.

def make_ood_data(sample_size=500, means=(2.5, -1.75), vars=(0.01, 0.01)):
  return np.random.multivariate_normal(
      means, cov=np.diag(vars), size=sample_size)

# Load the train, test and OOD datasets.
train_examples, train_labels = make_training_data(
    sample_size=500)
test_examples = make_testing_data()
ood_examples = make_ood_data(sample_size=500)

# Visualize
pos_examples = train_examples[train_labels == 0]
neg_examples = train_examples[train_labels == 1]

plt.figure(figsize=(7, 5.5))

plt.scatter(pos_examples[:, 0], pos_examples[:, 1], c="#377eb8", alpha=0.5)
plt.scatter(neg_examples[:, 0], neg_examples[:, 1], c="#ff7f00", alpha=0.5)
plt.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)

plt.legend(["Positive", "Negative", "Out-of-Domain"])

plt.ylim(DEFAULT_Y_RANGE)
plt.xlim(DEFAULT_X_RANGE)

plt.show()

Aquí, el azul y el naranja representan las clases positiva y negativa, y el rojo los datos OOD. Se espera que un modelo que cuantifique bien la incertidumbre sea seguro cuando esté cerca de los datos de entrenamiento (es decir, $p(x_{test})$ cerca de 0 o 1), y sea incierto cuando esté lejos de las regiones de datos de entrenamiento (es decir, $p(x_{test})$ cerca de 0.5).

El modelo determinístico

Definir modelo

Partimos del modelo determinista (línea de referencia): una red residual multicapa (ResNet) con regularización de abandono.

#@title
class DeepResNet(tf.keras.Model):
  """Defines a multi-layer residual network."""
  def __init__(self, num_classes, num_layers=3, num_hidden=128,
               dropout_rate=0.1, **classifier_kwargs):
    super().__init__()
    # Defines class meta data.
    self.num_hidden = num_hidden
    self.num_layers = num_layers
    self.dropout_rate = dropout_rate
    self.classifier_kwargs = classifier_kwargs

    # Defines the hidden layers.
    self.input_layer = tf.keras.layers.Dense(self.num_hidden, trainable=False)
    self.dense_layers = [self.make_dense_layer() for _ in range(num_layers)]

    # Defines the output layer.
    self.classifier = self.make_output_layer(num_classes)

  def call(self, inputs):
    # Projects the 2d input data to high dimension.
    hidden = self.input_layer(inputs)

    # Computes the ResNet hidden representations.
    for i in range(self.num_layers):
      resid = self.dense_layers[i](hidden)
      resid = tf.keras.layers.Dropout(self.dropout_rate)(resid)
      hidden += resid

    return self.classifier(hidden)

  def make_dense_layer(self):
    """Uses the Dense layer as the hidden layer."""
    return tf.keras.layers.Dense(self.num_hidden, activation="relu")

  def make_output_layer(self, num_classes):
    """Uses the Dense layer as the output layer."""
    return tf.keras.layers.Dense(
        num_classes, **self.classifier_kwargs)

Este tutorial usa una ResNet de seis capas con 128 unidades ocultas.

resnet_config = dict(num_classes=2, num_layers=6, num_hidden=128)

resnet_model = DeepResNet(**resnet_config)

resnet_model.build((None, 2))
resnet_model.summary()

Entrenar el modelo

Configure los parámetros de entrenamiento para usar SparseCategoricalCrossentropy como función de pérdida y el optimizador Adam.

loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.keras.metrics.SparseCategoricalAccuracy(),
optimizer = tf.keras.optimizers.legacy.Adam(learning_rate=1e-4)

train_config = dict(loss=loss, metrics=metrics, optimizer=optimizer)

Entrene el modelo durante 100 épocas con un tamaño de lote de 128.

fit_config = dict(batch_size=128, epochs=100)

resnet_model.compile(**train_config)
resnet_model.fit(train_examples, train_labels, **fit_config)

Visualizar la incertidumbre

#@title
def plot_uncertainty_surface(test_uncertainty, ax, cmap=None):
  """Visualizes the 2D uncertainty surface.
  
  For simplicity, assume these objects already exist in the memory:

    test_examples: Array of test examples, shape (num_test, 2).
    train_labels: Array of train labels, shape (num_train, ).
    train_examples: Array of train examples, shape (num_train, 2).
  
  Arguments:
    test_uncertainty: Array of uncertainty scores, shape (num_test,).
    ax: A matplotlib Axes object that specifies a matplotlib figure.
    cmap: A matplotlib colormap object specifying the palette of the
      predictive surface.

  Returns:
    pcm: A matplotlib PathCollection object that contains the palette
      information of the uncertainty plot.
  """
  # Normalize uncertainty for better visualization.
  test_uncertainty = test_uncertainty / np.max(test_uncertainty)

  # Set view limits.
  ax.set_ylim(DEFAULT_Y_RANGE)
  ax.set_xlim(DEFAULT_X_RANGE)

  # Plot normalized uncertainty surface.
  pcm = ax.imshow(
      np.reshape(test_uncertainty, [DEFAULT_N_GRID, DEFAULT_N_GRID]),
      cmap=cmap,
      origin="lower",
      extent=DEFAULT_X_RANGE + DEFAULT_Y_RANGE,
      vmin=DEFAULT_NORM.vmin,
      vmax=DEFAULT_NORM.vmax,
      interpolation='bicubic',
      aspect='auto')

  # Plot training data.
  ax.scatter(train_examples[:, 0], train_examples[:, 1],
             c=train_labels, cmap=DEFAULT_CMAP, alpha=0.5)
  ax.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)

  return pcm

Ahora visualice las predicciones del modelo determinista. Primero trace la probabilidad de clase: $$p(x) = softmax(logit(x))$$

resnet_logits = resnet_model(test_examples)
resnet_probs = tf.nn.softmax(resnet_logits, axis=-1)[:, 0]  # Take the probability for class 0.

_, ax = plt.subplots(figsize=(7, 5.5))

pcm = plot_uncertainty_surface(resnet_probs, ax=ax)

plt.colorbar(pcm, ax=ax)
plt.title("Class Probability, Deterministic Model")

plt.show()

En este gráfico, el amarillo y el morado son las probabilidades de predicción para las dos clases. El modelo determinista hizo un buen trabajo al clasificar las dos clases conocidas (azul y naranja) con un límite de decisión no lineal. Sin embargo, no es consciente de la distancia, y clasificó los ejemplos rojos nunca observados fuera del dominio (OOD) con confianza como la clase naranja.

Visualice la incertidumbre del modelo calculando la varianza predictiva: $$var(x) = p(x) * (1 - p(x))$$

resnet_uncertainty = resnet_probs * (1 - resnet_probs)

_, ax = plt.subplots(figsize=(7, 5.5))

pcm = plot_uncertainty_surface(resnet_uncertainty, ax=ax)

plt.colorbar(pcm, ax=ax)
plt.title("Predictive Uncertainty, Deterministic Model")

plt.show()

En este diagrama, el amarillo indica una incertidumbre alta y el morado una incertidumbre baja. La incertidumbre de una ResNet determinista sólo depende de la distancia de los ejemplos de prueba respecto al límite de decisión. Esto lleva al modelo a tener un exceso de confianza cuando se encuentra fuera del dominio de entrenamiento. La siguiente sección muestra cómo el SNGP se comporta de forma diferente en este conjunto de datos.

El modelo SNGP

Defina el modelo SNGP

Implementemos ahora el modelo SNGP. Los dos componentes SNGP, SpectralNormalization y RandomFeatureGaussianProcess, están disponibles en las capas built-in de tensorflow_model.

Inspeccionemos con más detalle estos dos componentes. (También puede pasar a la sección el modelo SNGP completo para saber cómo se implementa SNGP).

Envoltorio SpectralNormalization

SpectralNormalization{.externo} es un contenedor de capas Keras. Se puede aplicar a una capa Dense existente de esta manera:

dense = tf.keras.layers.Dense(units=10)
dense = nlp_layers.SpectralNormalization(dense, norm_multiplier=0.9)

La normalización espectral regulariza la ponderación oculta $W$ guiando gradualmente su norma espectral (es decir, el mayor valor propio de $W$) hacia el valor objetivo norm_multiplier).

Nota: Normalmente es preferible configurar norm_multiplier a un valor inferior a 1. Sin embargo, en la práctica, también se puede relajar a un valor superior para garantizar que la red profunda tenga suficiente poder de expresión.

La capa de Proceso Gaussiano (GP)

RandomFeatureGaussianProcess{.externo} implementa una aproximación basada en características aleatorias{.externo} a un modelo de proceso gaussiano que es entrenable de principio a fin con una red neuronal profunda. En el fondo, la capa del proceso gaussiano implementa una red de dos capas:

$$logits(x) = \Phi(x) \beta, \quad \Phi(x)=\sqrt{\frac{2}{M}} * cos(Wx + b)$$

Aquí, $x$ es la entrada, y $W$ y $b$ son ponderaciones congeladas inicializadas aleatoriamente a partir de distribuciones gaussiana y uniforme, respectivamente (por lo tanto, a $\Phi(x)$ se les llama "características aleatorias"). $\beta$ es la ponderación del núcleo aprendible similar a la de una capa Dense.

batch_size = 32
input_dim = 1024
num_classes = 10

gp_layer = nlp_layers.RandomFeatureGaussianProcess(units=num_classes,
                                               num_inducing=1024,
                                               normalize_input=False,
                                               scale_random_features=True,
                                               gp_cov_momentum=-1)

Los principales parámetros de las capas GP son:

• unidades: La dimensión de los logits de salida.

• num_inducing: La $M$ de dimensión de la ponderación oculta $W$. Por defecto es 1024.

• normalize_input: Si se aplica la normalización de capas a la entrada $x$.

• scale_random_features: Si se aplica la escala $\sqrt{2/M}$ a la salida oculta.

Nota: Para una red neuronal profunda que sea sensible a la tasa de aprendizaje (por ejemplo, ResNet-50 y ResNet-110), se recomienda generalmente configurar normalize_input=True para estabilizar el entrenamiento, y configurar scale_random_features=False para evitar que la tasa de aprendizaje se modifique de forma inesperada al pasar por la capa GP.

• gp_cov_momentum controla cómo se calcula la covarianza del modelo. Si se configura en un valor positivo (por ejemplo, 0.999), la matriz de covarianza se calcula usando la actualización promedio móvil basada en el momentum (similar a la normalización por lotes). Si se configura en -1, la matriz de covarianza se actualiza sin momentum.

Nota: El método de actualización basado en el momentum puede ser sensible al tamaño del lote. Por lo tanto, se recomienda configurar gp_cov_momentum=-1 para calcular la covarianza con exactitud. Para que esto funcione correctamente, el estimador de la matriz de covarianza debe reiniciarse al comienzo de una nueva época para evitar contar los mismos datos dos veces. Para RandomFeatureGaussianProcess, esto puede hacerse llamando a su reset_covariance_matrix(). La siguiente sección muestra una sencilla implementación de esto usando la API incorporada de Keras.

Dado un lote de entrada con forma (batch_size, input_dim), la capa GP devuelve un tensor logits (forma (batch_size, num_classes)) para la predicción, y también un tensor covmat (forma (batch_size, batch_size)) que es la matriz de covarianza posterior de los logits del lote.

embedding = tf.random.normal(shape=(batch_size, input_dim))

logits, covmat = gp_layer(embedding)

Nota: Observe que bajo esta implementación del modelo SNGP, los logits predictivos $logit(x_{test})$ para todas las clases comparten la misma matriz de covarianza $var(x_{test})$, que describe la distancia entre $x_{test}$ de los datos de entrenamiento.

Teóricamente, es posible ampliar el algoritmo para calcular diferentes valores de varianza para diferentes clases (como se presentó en el documento original de SNGP{.externo}). Sin embargo, esto es difícil de escalar para problemas con grandes espacios de salida (como la clasificación con ImageNet o el modelado del lenguaje).

El modelo SNGP completo

Dada la clase base DeepResNet, el modelo SNGP puede implementarse fácilmente modificando las capas ocultas y de salida de la red residual. Para que sea compatible con la API model.fit() de Keras, modifique también el método call() del modelo para que sólo emita logits durante el entrenamiento

class DeepResNetSNGP(DeepResNet):
  def __init__(self, spec_norm_bound=0.9, **kwargs):
    self.spec_norm_bound = spec_norm_bound
    super().__init__(**kwargs)

  def make_dense_layer(self):
    """Applies spectral normalization to the hidden layer."""
    dense_layer = super().make_dense_layer()
    return nlp_layers.SpectralNormalization(
        dense_layer, norm_multiplier=self.spec_norm_bound)

  def make_output_layer(self, num_classes):
    """Uses Gaussian process as the output layer."""
    return nlp_layers.RandomFeatureGaussianProcess(
        num_classes,
        gp_cov_momentum=-1,
        **self.classifier_kwargs)

  def call(self, inputs, training=False, return_covmat=False):
    # Gets logits and a covariance matrix from the GP layer.
    logits, covmat = super().call(inputs)

    # Returns only logits during training.
    if not training and return_covmat:
      return logits, covmat

    return logits

Usar la misma arquitectura que el modelo determinista.

resnet_config

sngp_model = DeepResNetSNGP(**resnet_config)

sngp_model.build((None, 2))
sngp_model.summary()

Implemente una retrollamada de Keras para restablecer la matriz de covarianza al comienzo de una nueva época.

class ResetCovarianceCallback(tf.keras.callbacks.Callback):

  def on_epoch_begin(self, epoch, logs=None):
    """Resets covariance matrix at the beginning of the epoch."""
    if epoch > 0:
      self.model.classifier.reset_covariance_matrix()

Añada esta retrollamada a la clase modelo DeepResNetSNGP.

class DeepResNetSNGPWithCovReset(DeepResNetSNGP):
  def fit(self, *args, **kwargs):
    """Adds ResetCovarianceCallback to model callbacks."""
    kwargs["callbacks"] = list(kwargs.get("callbacks", []))
    kwargs["callbacks"].append(ResetCovarianceCallback())

    return super().fit(*args, **kwargs)

Entrenar el modelo

Use tf.keras.model.fit para entrenar el modelo.

sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, **fit_config)

Visualizar la incertidumbre

Primero calcule los logaritmos predictivos y las varianzas.

sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)

sngp_variance = tf.linalg.diag_part(sngp_covmat)[:, None]

Ahora calcule la probabilidad predictiva posterior. El método clásico para calcular la probabilidad predictiva de un modelo probabilístico es usar el muestreo de Montecarlo, es decir,

$$E(p(x)) = \frac{1}{M} \sum_{m=1}^M logit_m(x),$$

donde $M$ es el tamaño de la muestra, y $logit_m(x)$ son muestreos aleatorios del $MultivariateNormal$(sngp_logits posterior al SNGP, sngp_covmat). Sin embargo, este enfoque puede resultar lento para aplicaciones sensibles a la latencia, como la conducción autónoma o las pujas en tiempo real. En su lugar, puede aproximar $E(p(x))$ usando el método de campo medio{.externo}:

$$E(p(x)) \approx softmax(\frac{logit(x)}{\sqrt{1+ \lambda * \sigma^2(x)}})$$

donde $\sigma^2(x)$ es la varianza SNGP, y $\lambda$ se selecciona a menudo como $\pi/8$ o $3/\pi^2$.

sngp_logits_adjusted = sngp_logits / tf.sqrt(1. + (np.pi / 8.) * sngp_variance)
sngp_probs = tf.nn.softmax(sngp_logits_adjusted, axis=-1)[:, 0]

Nota: En lugar de fijar $\lambda$ a un valor fijo, también puede tratarlo como un hiperparámetro, y afinarlo para optimizar el rendimiento de calibración del modelo. Esto se conoce como escalado de temperatura{.externo} en la literatura de incertidumbre del aprendizaje profundo.

Este método de campo medio se implementa como una función incorporada layers.gaussian_process.mean_field_logits:

def compute_posterior_mean_probability(logits, covmat, lambda_param=np.pi / 8.):
  # Computes uncertainty-adjusted logits using the built-in method.
  logits_adjusted = nlp_layers.gaussian_process.mean_field_logits(
      logits, covmat, mean_field_factor=lambda_param)
  
  return tf.nn.softmax(logits_adjusted, axis=-1)[:, 0]

sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)

Resumen SNGP

#@title

def plot_predictions(pred_probs, model_name=""):
  """Plot normalized class probabilities and predictive uncertainties."""
  # Compute predictive uncertainty.
  uncertainty = pred_probs * (1. - pred_probs)

  # Initialize the plot axes.
  fig, axs = plt.subplots(1, 2, figsize=(14, 5))

  # Plots the class probability.
  pcm_0 = plot_uncertainty_surface(pred_probs, ax=axs[0])
  # Plots the predictive uncertainty.
  pcm_1 = plot_uncertainty_surface(uncertainty, ax=axs[1])

  # Adds color bars and titles.
  fig.colorbar(pcm_0, ax=axs[0])
  fig.colorbar(pcm_1, ax=axs[1])

  axs[0].set_title(f"Class Probability, {model_name}")
  axs[1].set_title(f"(Normalized) Predictive Uncertainty, {model_name}")

  plt.show()  

Ahora puede combinarlo todo. Todo el procedimiento (entrenamiento, evaluación y cálculo de la incertidumbre) puede realizarse en sólo cinco líneas:

def train_and_test_sngp(train_examples, test_examples):
  sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)

  sngp_model.compile(**train_config)
  sngp_model.fit(train_examples, train_labels, verbose=0, **fit_config)

  sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
  sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)

  return sngp_probs

sngp_probs = train_and_test_sngp(train_examples, test_examples)

Visualice la probabilidad de clase (izquierda) y la incertidumbre predictiva (derecha) del modelo SNGP.

plot_predictions(sngp_probs, model_name="SNGP")

Recuerde que en el gráfico de probabilidad de clase (izquierda), el amarillo y el morado son probabilidades de clase. Cuando está cerca del dominio de los datos de entrenamiento, SNGP clasifica correctamente los ejemplos con una confianza alta (es decir, asignando una probabilidad cercana a 0 o 1). Cuando se aleja de los datos de entrenamiento, SNGP pierde gradualmente confianza y su probabilidad de predicción se acerca a 0.5, mientras que la incertidumbre (normalizada) del modelo se eleva a 1.

Compárelo con la superficie de incertidumbre del modelo determinista:

plot_predictions(resnet_probs, model_name="Deterministic")

Como ya se ha mencionado, un modelo determinista no es consciente de la distancia. Su incertidumbre viene definida por la distancia del ejemplo de prueba respecto al límite de decisión. Esto lleva al modelo a producir predicciones excesivamente seguras para los ejemplos fuera del dominio (rojo).

Comparación con otros enfoques de incertidumbre

Esta sección compara la incertidumbre de SNGP con el abandono de Monte Carlo{.externo} y Ensamble profundo{.externo}.

Ambos métodos se basan en el promedio de Monte Carlo de múltiples pasadas hacia delante de modelos deterministas. En primer lugar, configure el tamaño del ensamble $M$.

num_ensemble = 10

Abandono de Monte Carlo

Dada una red neuronal entrenada con capas de Abandono, el abandono de Monte Carlo calcula la probabilidad predictiva media

$$E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))$$

haciendo un promedio sobre múltiples pasadas hacia delante con Abandono ${logit_m(x)}_{m=1}^M$.

def mc_dropout_sampling(test_examples):
  # Enable dropout during inference.
  return resnet_model(test_examples, training=True)

# Monte Carlo dropout inference.
dropout_logit_samples = [mc_dropout_sampling(test_examples) for _ in range(num_ensemble)]
dropout_prob_samples = [tf.nn.softmax(dropout_logits, axis=-1)[:, 0] for dropout_logits in dropout_logit_samples]
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)

dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)

plot_predictions(dropout_probs, model_name="MC Dropout")

Ensamble profundo

Ensamble profundo es un método de última generación (pero costoso) para el aprendizaje profundo de incertidumbre. Para entrenar un ensamble profundo, primero hay que entrenar $M$ miembros del ensamble.

# Deep ensemble training
resnet_ensemble = []
for _ in range(num_ensemble):
  resnet_model = DeepResNet(**resnet_config)
  resnet_model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
  resnet_model.fit(train_examples, train_labels, verbose=0, **fit_config)

  resnet_ensemble.append(resnet_model)

Recopile logits y calcule la probabilidad predictiva media $E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))$.

# Deep ensemble inference
ensemble_logit_samples = [model(test_examples) for model in resnet_ensemble]
ensemble_prob_samples = [tf.nn.softmax(logits, axis=-1)[:, 0] for logits in ensemble_logit_samples]
ensemble_probs = tf.reduce_mean(ensemble_prob_samples, axis=0)

plot_predictions(ensemble_probs, model_name="Deep ensemble")

Tanto el método de Abandono de Monte Carlo como el de Ensamble profundo mejoran la capacidad de incertidumbre del modelo al hacer que el límite de decisión sea menos seguro. Sin embargo, ambos heredan la limitación de la red profunda determinista al carecer de conciencia de la distancia.

Resumen

En este tutorial, usted:

• Implementó el modelo SNGP en un clasificador profundo para mejorar su conocimiento de la distancia.

• Entrenó el modelo SNGP de principio a fin usando la API Model.fit de Keras.

• Visualizó el comportamiento de incertidumbre del SNGP.

• Comparó el comportamiento de la incertidumbre entre los modelos SNGP, de abandono de Monte Carlo y de ensamble profundo.

Recursos y lecturas complementarias

• Consulte el tutorial SNGP-BERT para ver un ejemplo de aplicación de SNGP en un modelo BERT para comprender el lenguaje natural con conocimiento de la incertidumbre.

• Vaya al repositorio de GitHub de Líneas de referencia de incertidumbre{.externo} para implementar el modelo SNGP (y muchos otros métodos de incertidumbre) en una amplia variedad de conjuntos de datos de referencia (por ejemplo, CIFAR, ImageNet, Detección de toxicidad de rompecabezas, etc.).

• Para una comprensión más profunda del método SNGP, consulte el artículo titulado Estimación de la incertidumbre simple y basada en principios con aprendizaje profundo determinista a través del conocimiento de la distancia{.externo}.