sngp.ipynb

Kernel: Python 3

Copyright 2021 The TensorFlow Authors.

#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

Aprendizado profundo com SNGP com reconhecimento de incerteza

Ver em TensorFlow.org

Executar no Google Colab

Ver no GitHub

Baixar notebook

Em aplicações de inteligência artificial críticas, como tomada de decisão médica e veículos autônomos, ou quando os dados têm ruído inerente (por exemplo, compreensão de língua natural), é importante que um classificador profundo quantifique a incerteza com confiança. O classificador profundo deve conseguir reconhecer suas próprias limitações e quando deve passar o controle para especialistas humanos. Este tutorial mostra como melhorar a capacidade de um classificador profundo de quantificar a incerteza usando uma técnica chamada Processo Gaussiano Neural normalizado espectral (SNGP, na sigla em inglês{.external}).

A ideia principal do SNGP é melhorar o reconhecimento de distância de um classificador profundo por meio de modificações simples da rede. O reconhecimento de distância de um modelo é uma medida de como sua probabilidade preditiva reflete a distância entre o exemplo de teste e os dados de treinamento. É uma propriedade desejável comum aos modelos probabilísticos padrão-ouro (por exemplo, o processo gaussiano{.external} com kernels RBF), mas que falta nos modelos com redes neurais profundas. O SNGP oferece uma maneira simples de incorporar esse comportamento de processo gaussiano a um classificador profundo, mantendo sua exatidão preditiva.

Este tutorial implementa um modelo de SNGP de rede residual profunda baseado em ResNet no dataset two moons do scikit-learn{.external} (duas Luas) e compara sua superfície de incerteza com a de duas outras estratégias de incerteza comuns: dropout de Monte Carlo{.external} e Ensemble profundo{.external}.

Este tutorial ilustra o modelo de SNGP em um dataset bidimensional de brinquedo. Para ver um exemplo de como aplicar o SNGP a uma tarefa real de compreensão de língua natural usando uma base BERT, confira o tutorial SNGP-BERT. Para ver implementações de alta qualidade de um modelo de SNGP (e muitos outros métodos de incerteza) em uma grande variedade de conjuntos referenciais (como CIFAR-100, ImageNet, Jigsaw toxicity detection, etc), confira o referencial Linhas de base de incerteza{.external}.

Sobre o SNGP

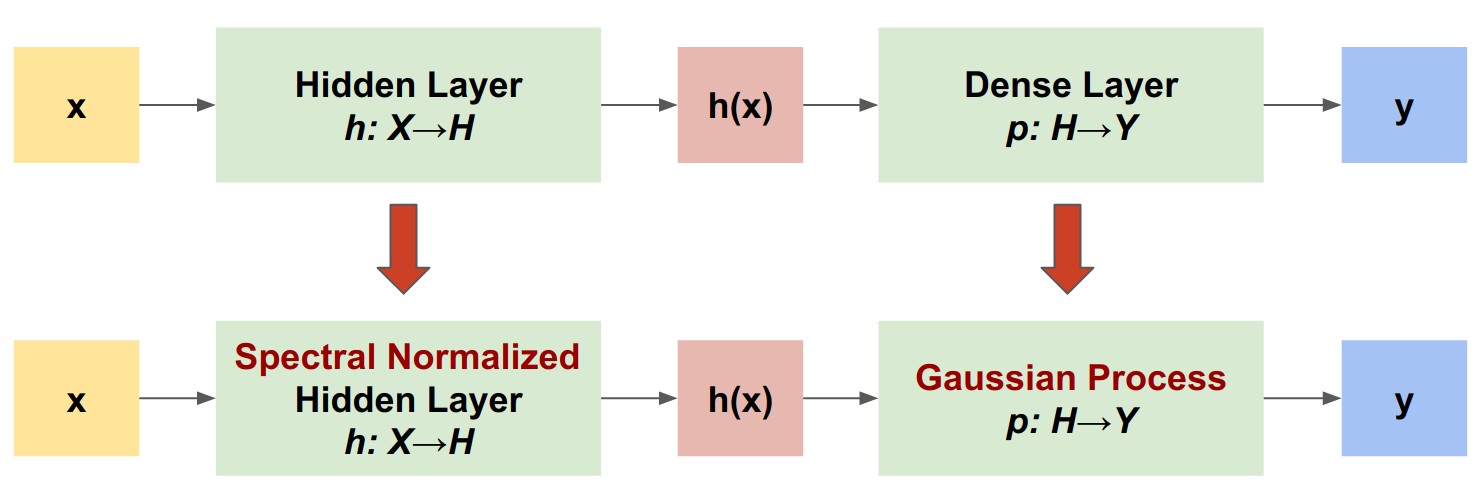
O SNGP é uma estratégia simples para melhorar a qualidade de incerteza de um classificador profundo mantendo um nível similar de exatidão e latência. Dada uma rede residual profunda, o SNGP faz duas alterações simples no modelo:

• Aplica a normalização espectral às camadas residuais ocultas.

• Substitui a camada de saída Dense por uma camada de processo gaussiano.

Comparado a outras estratégias de incerteza (como dropout de Monte Carlo e Ensemble profundo), o SNGP tem diversas vantagens:

• Funciona com diversas arquiteturas residuais de última geração (por exemplo, (Wide) ResNet, DenseNet ou BERT).

• É um método com um único modelo (não depende da média do ensemble). Portanto, o SNGP tem um nível similar de latência de uma única rede determinística e pode ser facilmente dimensionado para datasets grandes, como ImageNet{.external} e Jigsaw Toxic Comments classification{.external}.

• Tem um bom desempenho de detecção fora do domínio devido à propriedade de reconhecimento de distância.

As desvantagens deste método são:

• A incerteza preditiva do SNGP é computada usando-se o método de aproximação de Laplace{.external}. Portanto, teoricamente, a incerteza posterior do SNGP é diferente da de um processo gaussiano exato.

• O treinamento do SNGP requer uma etapa de redefinição da covariância no começo de uma nova época, o que pode adicionar uma pequena complexidade extra a um pipeline de treinamento. Este tutorial mostra uma forma simples de implementar isso usando callbacks do Keras.

Configuração

!pip install -U -q --use-deprecated=legacy-resolver tf-models-official tensorflow

# refresh pkg_resources so it takes the changes into account.
import pkg_resources
import importlib
importlib.reload(pkg_resources)

import matplotlib.pyplot as plt
import matplotlib.colors as colors

import sklearn.datasets

import numpy as np
import tensorflow as tf

import official.nlp.modeling.layers as nlp_layers

Defina as macros de visualização

plt.rcParams['figure.dpi'] = 140

DEFAULT_X_RANGE = (-3.5, 3.5)
DEFAULT_Y_RANGE = (-2.5, 2.5)
DEFAULT_CMAP = colors.ListedColormap(["#377eb8", "#ff7f00"])
DEFAULT_NORM = colors.Normalize(vmin=0, vmax=1,)
DEFAULT_N_GRID = 100

Dataset two moon (duas Luas)

Crie os datasets de treinamento e avaliação a partir do dataset two moon do scikit-learn{.external}.

def make_training_data(sample_size=500):
  """Create two moon training dataset."""
  train_examples, train_labels = sklearn.datasets.make_moons(
      n_samples=2 * sample_size, noise=0.1)

  # Adjust data position slightly.
  train_examples[train_labels == 0] += [-0.1, 0.2]
  train_examples[train_labels == 1] += [0.1, -0.2]

  return train_examples, train_labels

Avalie o comportamento preditivo do modelo para todo o espaço de entrada bidimensional.

def make_testing_data(x_range=DEFAULT_X_RANGE, y_range=DEFAULT_Y_RANGE, n_grid=DEFAULT_N_GRID):
  """Create a mesh grid in 2D space."""
  # testing data (mesh grid over data space)
  x = np.linspace(x_range[0], x_range[1], n_grid)
  y = np.linspace(y_range[0], y_range[1], n_grid)
  xv, yv = np.meshgrid(x, y)
  return np.stack([xv.flatten(), yv.flatten()], axis=-1)

Para avaliar a incerteza do modelo, adicione um dataset fora do domínio (OOD, na sigla em inglês) que pertença a uma terceira classe. O modelo nunca observa esses exemplos OOD durante o treinamento.

def make_ood_data(sample_size=500, means=(2.5, -1.75), vars=(0.01, 0.01)):
  return np.random.multivariate_normal(
      means, cov=np.diag(vars), size=sample_size)

# Load the train, test and OOD datasets.
train_examples, train_labels = make_training_data(
    sample_size=500)
test_examples = make_testing_data()
ood_examples = make_ood_data(sample_size=500)

# Visualize
pos_examples = train_examples[train_labels == 0]
neg_examples = train_examples[train_labels == 1]

plt.figure(figsize=(7, 5.5))

plt.scatter(pos_examples[:, 0], pos_examples[:, 1], c="#377eb8", alpha=0.5)
plt.scatter(neg_examples[:, 0], neg_examples[:, 1], c="#ff7f00", alpha=0.5)
plt.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)

plt.legend(["Positive", "Negative", "Out-of-Domain"])

plt.ylim(DEFAULT_Y_RANGE)
plt.xlim(DEFAULT_X_RANGE)

plt.show()

Aqui, azul e laranja representam as classes positivas e negativas, enquanto vermelho representa os dados OOD. Espera-se que um modelo que quantifique bem a incerteza tenha confiança quando próximo dos dados de treinamento (ou seja, $p(x_{test})$ próximo de 0 ou 1), e tenha incerteza quando distante das regiões dos dados de treinamento (ou seja, $p(x_{test})$ próximo de 0,5).

Modelo determinístico

Defina o modelo

Comece pelo modelo determinístico (linha de base): uma rede (ResNet) multicamada com regularização de dropout.

#@title
class DeepResNet(tf.keras.Model):
  """Defines a multi-layer residual network."""
  def __init__(self, num_classes, num_layers=3, num_hidden=128,
               dropout_rate=0.1, **classifier_kwargs):
    super().__init__()
    # Defines class meta data.
    self.num_hidden = num_hidden
    self.num_layers = num_layers
    self.dropout_rate = dropout_rate
    self.classifier_kwargs = classifier_kwargs

    # Defines the hidden layers.
    self.input_layer = tf.keras.layers.Dense(self.num_hidden, trainable=False)
    self.dense_layers = [self.make_dense_layer() for _ in range(num_layers)]

    # Defines the output layer.
    self.classifier = self.make_output_layer(num_classes)

  def call(self, inputs):
    # Projects the 2d input data to high dimension.
    hidden = self.input_layer(inputs)

    # Computes the ResNet hidden representations.
    for i in range(self.num_layers):
      resid = self.dense_layers[i](hidden)
      resid = tf.keras.layers.Dropout(self.dropout_rate)(resid)
      hidden += resid

    return self.classifier(hidden)

  def make_dense_layer(self):
    """Uses the Dense layer as the hidden layer."""
    return tf.keras.layers.Dense(self.num_hidden, activation="relu")

  def make_output_layer(self, num_classes):
    """Uses the Dense layer as the output layer."""
    return tf.keras.layers.Dense(
        num_classes, **self.classifier_kwargs)

Este tutorial utiliza uma ResNet de seis camadas, com 128 unidades ocultas.

resnet_config = dict(num_classes=2, num_layers=6, num_hidden=128)

resnet_model = DeepResNet(**resnet_config)

resnet_model.build((None, 2))
resnet_model.summary()

Treine o modelo

Configure os parâmetros de treinamento para usar SparseCategoricalCrossentropy como a função de perda e o otimizador Adam.

loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.keras.metrics.SparseCategoricalAccuracy(),
optimizer = tf.keras.optimizers.legacy.Adam(learning_rate=1e-4)

train_config = dict(loss=loss, metrics=metrics, optimizer=optimizer)

Treine o modelo com 100 épocas e tamanho de lote igual a 128.

fit_config = dict(batch_size=128, epochs=100)

resnet_model.compile(**train_config)
resnet_model.fit(train_examples, train_labels, **fit_config)

Visualize a incerteza

#@title
def plot_uncertainty_surface(test_uncertainty, ax, cmap=None):
  """Visualizes the 2D uncertainty surface.
  
  For simplicity, assume these objects already exist in the memory:

    test_examples: Array of test examples, shape (num_test, 2).
    train_labels: Array of train labels, shape (num_train, ).
    train_examples: Array of train examples, shape (num_train, 2).
  
  Arguments:
    test_uncertainty: Array of uncertainty scores, shape (num_test,).
    ax: A matplotlib Axes object that specifies a matplotlib figure.
    cmap: A matplotlib colormap object specifying the palette of the
      predictive surface.

  Returns:
    pcm: A matplotlib PathCollection object that contains the palette
      information of the uncertainty plot.
  """
  # Normalize uncertainty for better visualization.
  test_uncertainty = test_uncertainty / np.max(test_uncertainty)

  # Set view limits.
  ax.set_ylim(DEFAULT_Y_RANGE)
  ax.set_xlim(DEFAULT_X_RANGE)

  # Plot normalized uncertainty surface.
  pcm = ax.imshow(
      np.reshape(test_uncertainty, [DEFAULT_N_GRID, DEFAULT_N_GRID]),
      cmap=cmap,
      origin="lower",
      extent=DEFAULT_X_RANGE + DEFAULT_Y_RANGE,
      vmin=DEFAULT_NORM.vmin,
      vmax=DEFAULT_NORM.vmax,
      interpolation='bicubic',
      aspect='auto')

  # Plot training data.
  ax.scatter(train_examples[:, 0], train_examples[:, 1],
             c=train_labels, cmap=DEFAULT_CMAP, alpha=0.5)
  ax.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)

  return pcm

Agora, visualize as predições do modelo determinístico. Primeiro plote a probabilidade da classe: $$p(x) = softmax(logit(x))$$

resnet_logits = resnet_model(test_examples)
resnet_probs = tf.nn.softmax(resnet_logits, axis=-1)[:, 0]  # Take the probability for class 0.

_, ax = plt.subplots(figsize=(7, 5.5))

pcm = plot_uncertainty_surface(resnet_probs, ax=ax)

plt.colorbar(pcm, ax=ax)
plt.title("Class Probability, Deterministic Model")

plt.show()

Neste gráfico, amarelo e roxo são as probabilidades preditivas das duas classes. O modelo determinístico teve bom desempenho ao classificar as duas classes desconhecidas, azul e laranja, com um limite de decisão não linear. Entretanto, ele não tem reconhecimento de distância e classificou os exemplos fora do domínio (OOD) vermelhos, nunca observados antes, como a classe laranja com confiança.

Para visualizar a incerteza do modelo, calcule a variância preditiva: $$var(x) = p(x) * (1 - p(x))$$

resnet_uncertainty = resnet_probs * (1 - resnet_probs)

_, ax = plt.subplots(figsize=(7, 5.5))

pcm = plot_uncertainty_surface(resnet_uncertainty, ax=ax)

plt.colorbar(pcm, ax=ax)
plt.title("Predictive Uncertainty, Deterministic Model")

plt.show()

Neste gráfico, amarelo indica incerteza alta, e roxo indica incerteza baixa. A incerteza de uma ResNet determinística depende somente da distância entre os exemplos de teste e o limite de decisão. Isso faz o modelo ter uma confiança alta demais quando fora do domínio de treinamento. A próxima seção mostra como o SNGP se comporta de maneira diferente para este dataset.

Modelo de SNGP

Defina o modelo de SNGP

Agora, vamos implementar o modelo de SNGP. Os dois componentes do SNGP, SpectralNormalization e RandomFeatureGaussianProcess, estão disponíveis nas camadas integradas do modelo do TensorFlow.

Vamos avaliar esses dois componentes com mais detalhes (você também pode ir para a seção modelo de SNGP completo para ver como o SNGP é implementado).

Encapsulador SpectralNormalization

SpectralNormalization{.external} é um encapsulador de camadas do Keras e pode ser aplicado a uma camada Dense existente da seguinte forma:

dense = tf.keras.layers.Dense(units=10)
dense = nlp_layers.SpectralNormalization(dense, norm_multiplier=0.9)

A normalização espectral normaliza o peso oculto $W$ ao levar gradualmente sua norma espectral (ou seja, o autovalor mais alto de $W$) em direção ao valor alvo norm_multiplier.

Observação: geralmente, é preferível definir norm_multiplier como um valor menor do que 1. Entretanto, na prática, também pode ser definido como um valor mais alto para garantir que a rede profunda tenha potência expressiva suficiente.

Camada do processo gaussiano

RandomFeatureGaussianProcess{.external} implementa uma aproximação baseada em característica aleatória{.external} de um modelo de processo gaussiano que pode ser treinado do começo ao fim com uma rede neural profunda. Em segundo plano, a camada do processo gaussiano implementa uma rede de duas camadas:

$$logits(x) = \Phi(x) \beta, \quad \Phi(x)=\sqrt{\frac{2}{M}} * cos(Wx + b)$$

Aqui, $x$ é a entrada, e $W$ e $b$ são pesos congelados inicializados aleatoriamente a partir das distribuições gaussiana e uniforme, respectivamente (portanto, $\Phi(x)$ são chamadas de "características aleatórias"). $\beta$ é o peso de kernel que pode ser aprendido, similar ao de uma camada Dense.

batch_size = 32
input_dim = 1024
num_classes = 10

gp_layer = nlp_layers.RandomFeatureGaussianProcess(units=num_classes,
                                               num_inducing=1024,
                                               normalize_input=False,
                                               scale_random_features=True,
                                               gp_cov_momentum=-1)

Os principais parâmetros das camadas do processo gaussiano são:

• units: dimensão dos logits de saída.

• num_inducing: dimensão $M$ do peso oculto $W$. O padrão é 1024.

• normalize_input: define se a normalização da camada deve ser aplicada à entrada $x$.

• scale_random_features: define se a escala $\sqrt{2/M}$ deve ser aplicada à saída oculta.

Observação: para uma rede neural profunda sensível à taxa de aprendizado (por exemplo, ResNet-50 e ResNet-110), geralmente recomenda-se definir normalize_input=True para estabilizar o treinamento e definir scale_random_features=False para evitar que a taxa de aprendizado seja modificada de formas inesperadas ao passar pela camada do processo gaussiano.

• gp_cov_momentum controla como a covariância do modelo é calculada. Se definido como um valor positivo (por exemplo, 0.999), a matriz de covariância é calculada usando-se a atualização da média móvel baseada no momento (similar à normalização de lotes). Se definido como -1, a matriz de covariância é atualizada sem usar o momento.

Observação: o método de avaliação com base no momento pode ser sensível ao tamanho do lote. Portanto, geralmente recomenda-se definir gp_cov_momentum=-1 para calcular o valor exato da covariância. Para que isso funcione corretamente, o estimador da matriz de covariância precisa ser redefinido no começo de cada época para evitar a contabilização dos mesmos dados duas vezes. Para RandomFeatureGaussianProcess, isso pode ser feito realizando uma chamada a reset_covariance_matrix(). A próxima seção mostra uma implementação fácil usando a API integrada do Keras.

Dada uma entrada de lote com formato (batch_size, input_dim), a camada do processo gaussiano retorna um tensor logits (formato (batch_size, num_classes)) para a previsão, além de um tensor covmat (formato (batch_size, batch_size)), que é a matriz de covariância posterior dos logits do lote.

embedding = tf.random.normal(shape=(batch_size, input_dim))

logits, covmat = gp_layer(embedding)

Observação: com esta implementação do modelo de SNGP, os logits preditivos $logit(x_{test})$ de todas as classes compartilham a mesma matriz de covariância $var(x_{test})$, que descreve a distância entre $x_{test}$ e os dados de treinamento.

Teoricamente, é possível estender o algoritmo para calcular os diferentes valores de covariância para as diferentes classes (conforme discutido no artigo original sobre SNGP{.external}). Entretanto, é difícil fazer isso para problemas com espaços de saída grandes (como classificação com ImageNet ou modelagem de língua).

Modelo de SNGP completo

Dada a classe base DeepResNet, é fácil implementar o modelo de SNGP por meio da modificação das camadas ocultas e da saída da rede residual. Para fins de compatibilidade com a API model.fit() do Keras, modifique também o método call() do modelo para que gere somente os logits durante o treinamento.

class DeepResNetSNGP(DeepResNet):
  def __init__(self, spec_norm_bound=0.9, **kwargs):
    self.spec_norm_bound = spec_norm_bound
    super().__init__(**kwargs)

  def make_dense_layer(self):
    """Applies spectral normalization to the hidden layer."""
    dense_layer = super().make_dense_layer()
    return nlp_layers.SpectralNormalization(
        dense_layer, norm_multiplier=self.spec_norm_bound)

  def make_output_layer(self, num_classes):
    """Uses Gaussian process as the output layer."""
    return nlp_layers.RandomFeatureGaussianProcess(
        num_classes,
        gp_cov_momentum=-1,
        **self.classifier_kwargs)

  def call(self, inputs, training=False, return_covmat=False):
    # Gets logits and a covariance matrix from the GP layer.
    logits, covmat = super().call(inputs)

    # Returns only logits during training.
    if not training and return_covmat:
      return logits, covmat

    return logits

Utilize a mesma arquitetura usada no modelo determinístico:

resnet_config

sngp_model = DeepResNetSNGP(**resnet_config)

sngp_model.build((None, 2))
sngp_model.summary()

Implemente um callback do Keras para redefinir a matriz de covariância no começo de uma nova época:

class ResetCovarianceCallback(tf.keras.callbacks.Callback):

  def on_epoch_begin(self, epoch, logs=None):
    """Resets covariance matrix at the beginning of the epoch."""
    if epoch > 0:
      self.model.classifier.reset_covariance_matrix()

Adicione esse callback à classe do modelo DeepResNetSNGP.

class DeepResNetSNGPWithCovReset(DeepResNetSNGP):
  def fit(self, *args, **kwargs):
    """Adds ResetCovarianceCallback to model callbacks."""
    kwargs["callbacks"] = list(kwargs.get("callbacks", []))
    kwargs["callbacks"].append(ResetCovarianceCallback())

    return super().fit(*args, **kwargs)

Treine o modelo

Use tf.keras.model.fit para treinar o modelo.

sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, **fit_config)

Visualize a incerteza

Primeiro, calcule as variâncias e os logits preditivos.

sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)

sngp_variance = tf.linalg.diag_part(sngp_covmat)[:, None]

Agora, calcule a probabilidade preditiva posterior. O método clássico para calcular a probabilidade preditiva de um modelo probabilístico é usando a amostragem de Monte Carlo:

$$E(p(x)) = \frac{1}{M} \sum_{m=1}^M logit_m(x),$$

em que $M$ é o tamanho da amostra, e $logit_m(x)$ são amostras aleatórias do $MultivariateNormal$(sngp_logits posterior do SNGP, sngp_covmat). Entretanto, essa estratégia pode ser lenta demais para aplicações sensíveis à latência, como veículos autônomos ou leilão em tempo real. Em vez disso, você pode aproximar $E(p(x))$ usando o método do campo médio{.external}:

$$E(p(x)) \approx softmax(\frac{logit(x)}{\sqrt{1+ \lambda * \sigma^2(x)}})$$

em que $\sigma^2(x)$ é a variância do SNGP, e $\lambda$ geralmente é escolhido como $\pi/8$ ou $3/\pi^2$.

sngp_logits_adjusted = sngp_logits / tf.sqrt(1. + (np.pi / 8.) * sngp_variance)
sngp_probs = tf.nn.softmax(sngp_logits_adjusted, axis=-1)[:, 0]

Observação: em vez de fixar $\lambda$, você também pode tratá-lo como um hiperparâmetro para otimizar o desempenho de calibração do modelo. Isso é conhecido como Temperature Scaling{.external} (dimensionamento de temperatura) na literatura sobre incerteza em aprendizado profundo.

Esse método do campo médio é implementado como uma função integrada layers.gaussian_process.mean_field_logits:

def compute_posterior_mean_probability(logits, covmat, lambda_param=np.pi / 8.):
  # Computes uncertainty-adjusted logits using the built-in method.
  logits_adjusted = nlp_layers.gaussian_process.mean_field_logits(
      logits, covmat, mean_field_factor=lambda_param)
  
  return tf.nn.softmax(logits_adjusted, axis=-1)[:, 0]

sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)

Resumo do SNGP

#@title

def plot_predictions(pred_probs, model_name=""):
  """Plot normalized class probabilities and predictive uncertainties."""
  # Compute predictive uncertainty.
  uncertainty = pred_probs * (1. - pred_probs)

  # Initialize the plot axes.
  fig, axs = plt.subplots(1, 2, figsize=(14, 5))

  # Plots the class probability.
  pcm_0 = plot_uncertainty_surface(pred_probs, ax=axs[0])
  # Plots the predictive uncertainty.
  pcm_1 = plot_uncertainty_surface(uncertainty, ax=axs[1])

  # Adds color bars and titles.
  fig.colorbar(pcm_0, ax=axs[0])
  fig.colorbar(pcm_1, ax=axs[1])

  axs[0].set_title(f"Class Probability, {model_name}")
  axs[1].set_title(f"(Normalized) Predictive Uncertainty, {model_name}")

  plt.show()  

Agora você pode juntar tudo. Todo o procedimento — treinamento, avaliação e cálculo da incerteza — pode ser feito em apenas cinco linhas:

def train_and_test_sngp(train_examples, test_examples):
  sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)

  sngp_model.compile(**train_config)
  sngp_model.fit(train_examples, train_labels, verbose=0, **fit_config)

  sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
  sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)

  return sngp_probs

sngp_probs = train_and_test_sngp(train_examples, test_examples)

Visualize a probabilidade das classes (à esquerda) e a incerteza preditiva (à direita) do modelo de SNGP.

plot_predictions(sngp_probs, model_name="SNGP")

Lembre-se de que, no gráfico de probabilidades de classes (à esquerda), amarelo e roxo são as probabilidades das classes. Quando próximo do domínio dos dados de treinamento, o SNGP classifica corretamente os exemplos com confiança alta (ou seja, atribuição perto da probabilidade 0 ou 1). Quando distante dos dados de treinamento, o SNGP fica cada vez mais menos confiante, e sua probabilidade preditiva se aproxima de 0,5, enquanto a incerteza do modelo (normalizada) sobe para 1.

Compare com a superfície de incerteza do modelo determinístico:

plot_predictions(resnet_probs, model_name="Deterministic")

Conforme mencionado anteriormente, um modelo determinístico não tem reconhecimento de distância. Sua incerteza é definida pela distância entre o exemplo de teste e o limite de decisão. Isso faz o modelo gerar previsões com confiança alta demais para os exemplos fora do domínio (vermelhos).

Comparação com outras estratégias de incerteza

Esta seção compara a incerteza do SNGP com Dropout de Monte Carlo{.external} e Ensemble profundo{.external}.

Os dois métodos são baseados na média de Monte Carlo de diversos passos para frente de modelos determinísticos. Primeiro, defina o tamanho do ensemble $M$.

num_ensemble = 10

Dropout de Monte Carlo

Dada uma rede neural treinada com camadas de dropout, o dropout de Monte Carlo calcula a probabilidade preditiva média:

$$E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))$$

fazendo a média de diversos passos para frente com dropout ${logit_m(x)}_{m=1}^M$.

def mc_dropout_sampling(test_examples):
  # Enable dropout during inference.
  return resnet_model(test_examples, training=True)

# Monte Carlo dropout inference.
dropout_logit_samples = [mc_dropout_sampling(test_examples) for _ in range(num_ensemble)]
dropout_prob_samples = [tf.nn.softmax(dropout_logits, axis=-1)[:, 0] for dropout_logits in dropout_logit_samples]
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)

dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)

plot_predictions(dropout_probs, model_name="MC Dropout")

Ensemble profundo

O ensemble profundo é um método de última geração (porém caro) para incerteza em aprendizado profundo. Para treinar um ensemble profundo, primeiro treine os membros do ensemble $M$.

# Deep ensemble training
resnet_ensemble = []
for _ in range(num_ensemble):
  resnet_model = DeepResNet(**resnet_config)
  resnet_model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
  resnet_model.fit(train_examples, train_labels, verbose=0, **fit_config)

  resnet_ensemble.append(resnet_model)

Colete os logits e calcule a probabilidade preditiva média $E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))$.

# Deep ensemble inference
ensemble_logit_samples = [model(test_examples) for model in resnet_ensemble]
ensemble_prob_samples = [tf.nn.softmax(logits, axis=-1)[:, 0] for logits in ensemble_logit_samples]
ensemble_probs = tf.reduce_mean(ensemble_prob_samples, axis=0)

plot_predictions(ensemble_probs, model_name="Deep ensemble")

Tanto o método de dropout de Monte Carlo quanto o de ensemble profundo melhoram a capacidade de incerteza do modelo ao diminuir a certeza do limite de decisão. Entretanto, ambos herdam a limitação de redes profundas determinísticas: a falta de reconhecimento de distância.

Resumo

Neste tutorial, você:

• Implementou o modelo de SNGP em um classificador profundo para melhorar seu reconhecimento de distância.

• Treinou o modelo de SNGP do começo ao fim usando a API Model.fit do Keras.

• Visualizou o comportamento da incerteza do SNGP.

• Comparou o comportamento da incerteza entre os modelos de SNGP, dropout de Monte Carlo e ensemble profundo.

Recursos e leitura adicional

• Confira o tutorial SNGP-BERT para ver um exemplo de como aplicar o SNGP a um modelo BERT para a compreensão de língua natural com reconhecimento de incerteza.

• Acesse o repositório do GitHub Linhas de base de incerteza{.external} para ver a implementação do modelo de SNGP (e muitos outros métodos de incerteza) para uma variedade de datasets referenciais (por exemplo, CIFAR, ImageNet, Jigsaw toxicity detection, etc).

• Para ter uma compreensão mais profunda do método do SNGP, confira o artigo Estimativa simples do princípio da incerteza com aprendizado profundo determinístico via reconhecimento de distância{.external}.