Introdução Linguagem Python para física experimental.ipynb

Kernel: Python 3 (Anaconda 2021)

This notebook was created by João Marcello Pereira, and is licensed under Creative Commons BY-SA

Objetivo do tutorial

Este guia serve apenas para você aprender conceitos básicos da linguagem Python para serem utilizados nos cálculos estatísticos e cálculos com incertezas de medição e propagação de incertezas. Para aprender mais sobre a linguagem baixe os arquivos em: https://bit.ly/tutorial-basico-python-julia-fisica. As versões mais atuais deste tutorial podem ser encontradas para download em https://bit.ly/fisica-experimental.

Linguagem Python

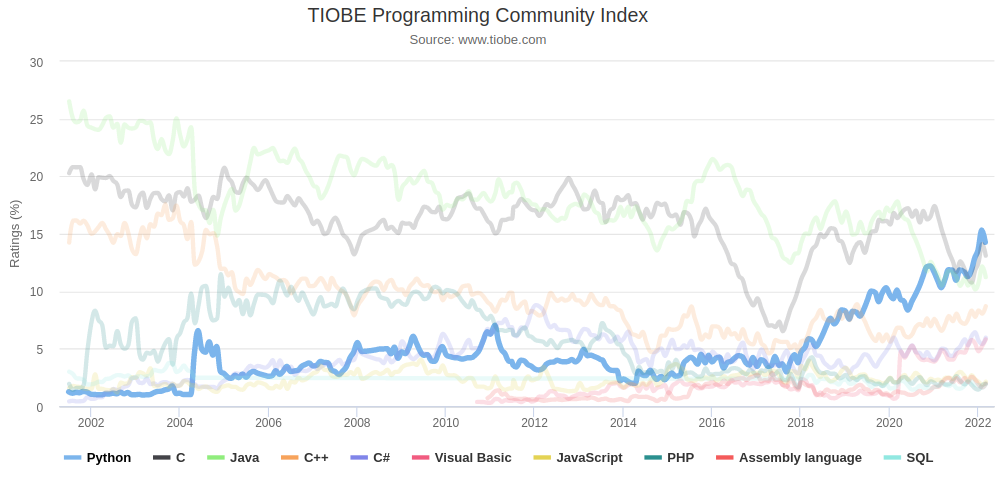
A linguagem de progração Python vem crescendo há anos e atualmente é uma das mais utilizadas no mundo conforme gráfico da TIOBE (https://www.tiobe.com/tiobe-index/). Observe que a linha azul está crescente enquanto as outras estão estabilizadas (C, C++ e SQL por exemplo) ou em queda (Java e PHP por exemplo).

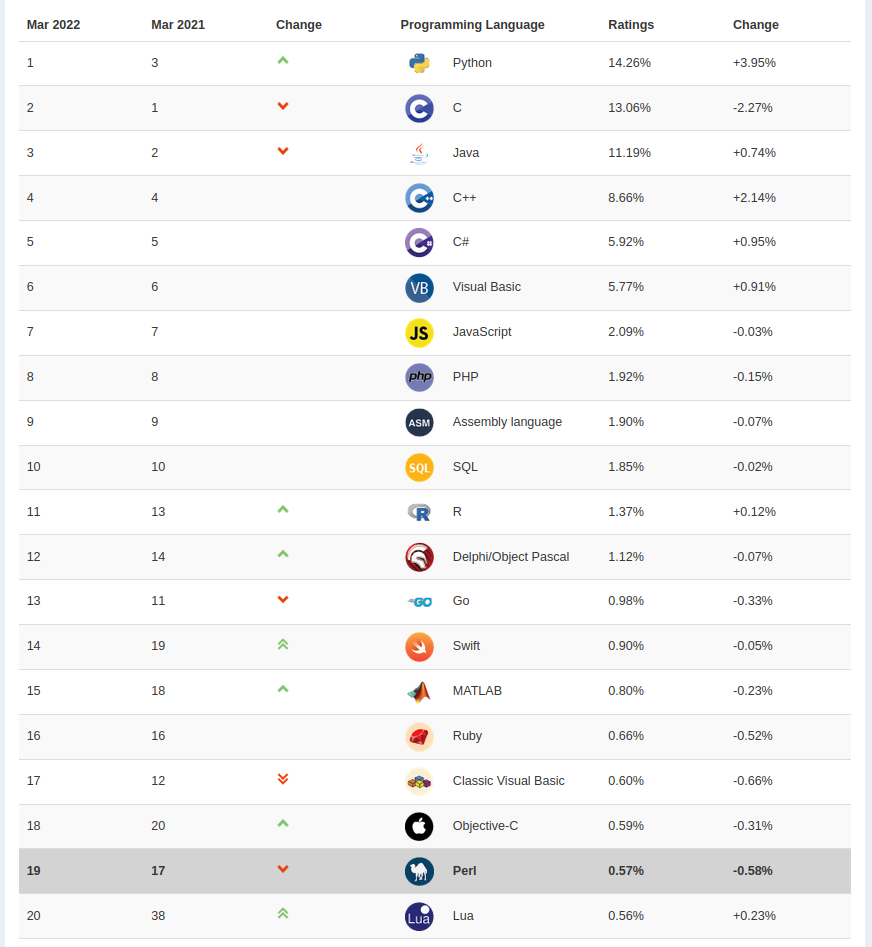
Além disso, de acordo com o ranking das melhores linguagens mais populares de março de 20200, mostra Python como primeira colocada seguida de C e Java.

Em relação aos cursos de engenharia, os artigos abaixo esclarecem melhor a razão da necessidade do engenheiro aprender Python:

https://www.voitto.com.br/blog/artigo/python-para-engenheiros

https://engenharia360.com/linguagem-python-na-engenharia/

Parte I

A ideia deste tutorial não é fazer o aluno apredender a programar na linguagem Python, mas sim ensiná-lo a operar comandos de cálculos estatísticas e de incerteza de medidas como uma calculadora avançada. Caso queira aprender Python há um excelente material neste link: https://bit.ly/tutorial-basico-python-julia-fisica. As versões mais atuais deste tutorial podem ser encontradas para download em https://bit.ly/fisica-experimental.

Conhecimentos inicias da linguagem

• Python é case-sensitive, ou seja, variáveis com nomes maiúsculos e minúsculos são diferentes;

    Peso e peso -> são variáveis diferentes    
  

• NÃO USE NOMES COM ACENTOS OU OUTROS RECURSOS SINTÁTICOS DA LINGUA PORTUGUESA PARA VARIÁVEIS. Apesar de funcionar no Jupyter, nem todos os interpretadores garantem a funcionalidade;

    posição -> Errado!
    posicao -> Certo.        
  

• Python é uma linguagem de tipagem dinâmica, logo o tipo de dado é definido quando o valor é atriuído a uma variável;

    a = 5   {tipo inteiro}
    a = 5.0 {tipo float}        
  

• Não é necessário ponto e vírgula ao final de um comando. Se fizer isso, o resultado do cálculo será omitido;

• A identação é essencial na linguagem mas segui-la garante uma boa organização do código;

    Errado: 
        def funcao(x):
        return 2*x
    
    Correto:
        def funcao(x):
            return 2*x
  

  Observe que há um recúo antes da palavra return

• Estamos usando uma inte

Conhecimentos inicias da interface Web Jupyter Notebook

O Jupyter é uma aplicação web derivado do IPython que significa JUlia, PYThon, and R . Resumidamente, é um ambiente computacional interativo que permite aos usuários criar "notebooks" que incluem: código, widgets interativos, gráficos, texto, equações, imagens, vídeo e outros. O Jupyter combina três componentes:

• O Jupyter Notebook: um aplicativo web interativo para escrever e executar códigos de várias linguagens de programação.

• Kernels: "Os kernels são processos específicos de linguagem de programação que funcionam independentemente e interagem com os aplicativos Jupyter e suas interfaces de usuário" (JUPYTER, 2017). Jupyter possui suporte para mais de 50 linguagens de programação (github.com/jupyter/jupyter/wiki/Jupyter-kernels), incluindo as mais populares em computação científica como Python, R, Julia e Scala. O IJulia.jl é kernel da linguagem Julia.

• Notebooks: são arquivos com extensão ipynb que contêm a estrutura do código no formato JSON. Cada notebook possui seu próprio kernel.

Caracteristicas:

• Instalação fácil, já está presente no Anaconda (www.anaconda.com/download) e disponível para as plataformas Windows, Linux e MacOS.

• Possui uma interface web avançada que permite combinar código-fonte, textos, fórmulas, figuras e multimídia em um único documento.

• Pode ser executado em um computador local ou servidor remoto.

• Suporta mais de 50 linguagens de programação, entre os quais R, Julia e Scala.

• Permite compartilhar documentos.

• Podemos executar e visualizar imagens, vídeos, textos LaTeX e Markdown, além de manipular os resultados em tempo real.

• Documentos feitos em Jupyter Notebook podem ser exportados para diferentes formatos (PDF, HTML, reStructeredText, LaTeX, Slides, Markdown e outros)

Para aprender sobre interface Jupyter Notebook, acesse este vídeo: https://www.youtube.com/watch?v=dPb4acFiaYs

Comandos básicos

Matemática elementar

# soma e subtração. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

2.0 + 5.0

7.0

# treino: calcule 589.01 + 2.56

# soma e subtração. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

2.0 - 5.0

# treino: calcule 589.01 - 2.56

# multiplicação e divisão. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

2.0 * 5.0

# treino: calcule 589.01 * 2.56

# multiplicação e divisão. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

2.0 / 5.0

# treino: calcule 589.01 dividido por 2.56

# potenciação e logarítmo. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

2.0^3.0

# treino: calcule 5.9 elevado a -2

# potenciação e logarítmo. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

exp(2)

# treino: calcule 'e' elevado a -3

# potenciação e logarítmo. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

exp(2.0)

# treino: calcule exponencial e -3

# potenciação e logarítmo. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

log(100.0, 10)

# treino: calcule logaritimo de 20000 na base 10 e na base 2

Trigonometria

Na linguagem Python, o cálculo das funções trigonométricas são feitos em radianos. Para converter para um ângulo de grau para radinao, devemos importar a função radians(valor_grau) do pacote math

# importar pacote 
# apenas execute com shit+enter ou execute run

from math import *

# seno de 30 radianos. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

sin(30.0)

# treino: calcule o seno de 60 radianos

# seno de 30 graus. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

sin(radians(30.0))

# treino: calcule o seno de 60º

# cosseno de 30 graus. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

cos(radians(30.0))

# treino: calcule o cosseno de 60º

# tangente de 30 graus. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

tan(radians(30.0))

# treino: calcule a tangente de 60º

As funções arco, ou funções trigonométricas inversas, retornan o valor correspondente, em graus ou radianos, do número calculado. São denotadas por asin(), acos(), atan(), etc.

# calcular o angulo em radianos do arco seno de 0.5. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

asin(0.5)

# treino: calcular o angulo em radianos do arco seno de 0.74. 

# calcular o angulo em graus do arco seno de 0.5. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

degrees(asin(0.5))

# treino: calcular o angulo em graus do arco seno de 0.74. 

# calcular o angulo em graus do arco cosseno de 0.5.
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

degrees(acos(0.5))

# treino: calcule o angulo do arco cosseno de 0.74

# calcular o angulo em graus do arco tangente de 0.5.
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

degrees(atan(0.5))

# treino: calcular o angulo em radianos do arco tangente0 de 0.74. 

Instalação de pacotes

# instalar pacotes. Se ja instalou não precisa instalar novamente
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

!pip install pandas
!pip install uncertainties

Defaulting to user installation because normal site-packages is not writeable
Requirement already satisfied: pandas in /ext/anaconda2021.11/lib/python3.9/site-packages (1.3.4)
Requirement already satisfied: python-dateutil>=2.7.3 in /ext/anaconda2021.11/lib/python3.9/site-packages (from pandas) (2.8.2)
Requirement already satisfied: pytz>=2017.3 in /ext/anaconda2021.11/lib/python3.9/site-packages (from pandas) (2021.3)
Requirement already satisfied: numpy>=1.17.3 in /ext/anaconda2021.11/lib/python3.9/site-packages (from pandas) (1.20.3)
Requirement already satisfied: six>=1.5 in /ext/anaconda2021.11/lib/python3.9/site-packages (from python-dateutil>=2.7.3->pandas) (1.16.0)
Defaulting to user installation because normal site-packages is not writeable
Requirement already satisfied: uncertainties in /ext/anaconda2021.11/lib/python3.9/site-packages (3.1.6)
Requirement already satisfied: future in /ext/anaconda2021.11/lib/python3.9/site-packages (from uncertainties) (0.18.2)
Defaulting to user installation because normal site-packages is not writeable
ERROR: You must give at least one requirement to install (see "pip help install")

Baixe o arquivo FexIFC.py. Coloque este arquivo na mesma pasta do arquivo ipynb.

Função

Basicamente, uma função em qualquer linguagem de programação, segue um conceito semelhante a uma função definida na matemática, no qual devemos substituir valores de uma variável em uma expressão algébrica e ela calcula o valor de saída. Dessa forma, podemos entender que uma função em uma linguagem de programação é como se fosse uma pequena "máquina" que recebe valores de entrada (chamados de argumentos), processa esses valores e devolve (return) um valor de saída.

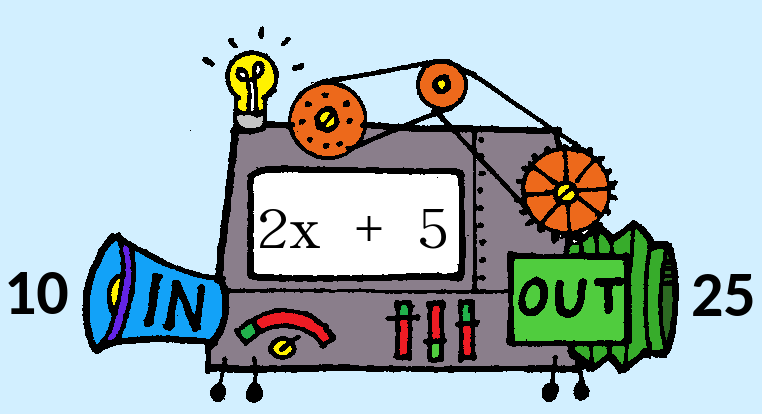
Na linguagem Python, uma função segue o seguinte esquema:

def nome_função(argumento_1, argumento_2, argumento_3, ...., argumento_n):
    return expressão_algébrica_dos_argumentos

Exemplo 1

Criar uma função que calcule $f (5)$, sendo $f(x) = 2x^2 - 3x +2$.

# criar a função
def f(x):
    return 2*x**2 - 3*x + 2

# testar para f(5)
f(5)

37

Exemplo 2

Criar uma função que calcule o volume de um bloco retangular de cimento. Medidas: largura = 5,0cm, comprimento = 12,0 cm e altura = 7,0 cm.

# criar a função volume
def v(l, c, h):
    return l*c*h

# testar para as medidas
v(5,12,7)

420

Cálculo com incertezas com dados não repetidos

Incerteza de medida com equipamentos analógicos e digitais

Quando se faz uma medida com algum equipamento de medida, sempre há uma incerteza associada à medida realizada conforme o tipo de equipamentos utilizado. Uma medida é definida como:

medida = ($m \pm \Delta m$) sendo:

• $m$ -> medida realizada por um instrumento de medida

• $\Delta m$ -> incerteza da escala ou de medição do instrumento de medida

A incerteza da escala ou de medição depende do equipamento e cada um pode apresentar uma maior ou menor incerteza. e quanto menor a incerteza melhor a medição. A incerteza $\Delta m$ depende da natureza tecnológica do instrumento.

De acordo com o equipamento, podemos observar que quanto menor a incerteza, melhor a precisão da medida. O GUM (Guia para a Expressão de Incerteza de Medição) informa que:

É geralmente suficiente fornecer a incerteza com até no máximo dois algarismos significativos, embora, em alguns casos, seja necessário reter algarismos adicionais para evitar erros de arredondamento nos cálculos subsequentes.

Equipamentos de medida analógicos

De acordo com PIACENTINI et al (2012) a incerteza de escala em equipamentos analógicos é dado por:

$~~~~~~~~~~ \displaystyle \Delta{m} = \frac{\text{menor divisão da escala}}{2}$

Para uma régua ou trena comum, a menor divisão de escala é de 1mm (0,01 cm), logo, a incerteza da escala de medição é: $~~\displaystyle \Delta{m} = \frac{0,1 cm}{2} = 0,05cm$. A medida do comprimento do parafuso da figura medido com esta régua, apresenta medida definida como:

ParseError: KaTeX parse error: Expected 'EOF', got '_' at position 18: …ext{comprimento_̲parafuso} = (2,…

Equipamentos de medida não analógico:

De acordo com PIACENTINI et al (2012) a incerteza de escala em equipamentos não-analógicos é dado por:

$~~~~~~~~~~ \displaystyle \Delta{m} = \text{menor divisão da escala}$

Para um paquímetro, a incerteza da escala é $~~\displaystyle \Delta{m} = 0.005 cm$

Propagação de incertezas

Quando obtemos medidas, é natural utilizá-las em alguma equação ou função. Sabendo que cada medida há uma incerteza de medida, a propagação de incerteza de uma função $f(x, y, z, ..., w)$ que relaciona várias grandezas $x, y, z ...w$, cada uma definida como $x = \bar x \pm \Delta x$, $y = \bar y \pm \Delta y$, ..., $w = \bar w \pm \Delta w$. A incerteza do cálculo realizado com esta função será dada pela raiz quadrada dos quadrados das derivadas parciais das grandezas mutiplicado pelo quadrado das incertezas:

$~~~~~~~~~~\displaystyle \Delta m={\sqrt {\left({\frac {\partial f}{\partial {x}}}\right)^{2}(\Delta x)^{2}+\left({\frac {\partial f}{\partial {y}}}\right)^{2}(\Delta y)^{2}+... +\left({\frac {\partial f}{\partial {w}}}\right)^{2}(\Delta w)^{2}}}$

Exemplo 3

Como calcular a área da base e o volume do cubo abaixo

$L = (22.00 \pm 0.05)cm$ $~~~~~C = (20.00\pm 0.05)cm$ $~~~~~ h = (9.00 \pm 0.05)cm$

$~$

$A(L,C) = L\cdot C$

$A(L,C) = 22,00\cdot 20,00 = 440cm²$

$~$

${\displaystyle {\left({\frac {\partial A}{\partial {L}}}\right)^{2}}} = C^2 = 20,00^2 = 400,00 cm^2$

${\displaystyle {\left({\frac {\partial A}{\partial {C}}}\right)^{2}}} = L^2 = 22,00^2 = 484,00cm^2$

$(\Delta x)^{2} = 0,05^2 = 0,0025$

$(\Delta y)^{2} = 0,05^2 = 0,0025$

$~$

$\Delta A = \displaystyle \sqrt{400,00 \cdot 0,0025 + 484,00 \cdot 0,0025}$

$\Delta A = 1,48660687473 cm^2$

$\Delta A = 1,5 cm^2$

$~$

$A = (440,0 \pm 1,5)cm²$

# carregar a função 'ufloat' do pacote de cálculo de inceretzas
# apenas execute shit+enter no teclado ou toque em Run

from uncertainties import *

# definir as variáveis. 
# apenas execute shit+enter no teclado ou toque em Run

L = ufloat(22.00, 0.05)
C = ufloat(20.00, 0.05)
h = ufloat(9.00, 0.05)

print(f"largura : {L}")
print(f"comprimento : {C}")
print(f"altura : {h}")

largura : 22.00+/-0.05
comprimento : 20.00+/-0.05
altura : 9.00+/-0.05

# calcular a área da base da figura geométrica. 
# apenas execute shit+enter no teclado ou toque em Run

A = L*C
A

440.0+/-1.4866068747318506

# para imprimir o resultado já com 2 Algarismos significativos
# apenas execute shit+enter no teclado ou toque em Run

print(f"altura : {A}")

altura : 440.0+/-1.5

# calcular o volume.
# apenas execute shit+enter no teclado ou toque em Run

V = L*C*h
V

3960.0+/-25.7489805623446

# treino:
# calcular o volume em m² de um cilindro medido com régua de raio (50.00 +/- 0.05)cm e altura (30 +/- 0.05)cm

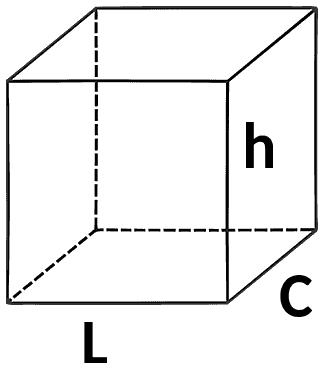
Exemplo 4

Como exemplo, vamos calcular a área frontal e o volume do cubo acima.

# carregar pacotes
# apenas execute shit+enter no teclado ou toque em Run

from numpy import *
from uncertainties import *

# Função área da base. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

def area(largura, comprimento):
    return print(f"{largura*comprimento}")

# calcular a área
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

area(ufloat(20.00, 0.05), ufloat(20.00, 0.05))

400.0+/-1.4

# Função volume. 
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

def volume(largura, comprimento, profundidade):
    return print(f"{largura*comprimento*profundidade}")

# calcular a área
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

volume(ufloat(20.0, 0.05), ufloat(20.00, 0.05), ufloat(9.00, 0.05))

3600+/-24

# treino:
# calcular o volume em m² de um cilindro medido com régua de raio (50.00 +/- 0.05)cm e altura (30 +/- 0.05)cm

Cálculo com equações e sistemas lineares e não lineares

Exemplo 5

Calcular a raiz da função $f(x) = a \cdot x^2 + b \cdot x + c$, sendo $a = 1.00 \pm 0.01$, $~b = 2.00 \pm 0.01$ e $~c = -4.00 \pm 0.01$

# carregar pacotes
from FexIFC import *

# definir a função
# apenas execute shit+enter no teclado ou toque em Run

def f(x):
    return ufloat(1.00, 0.01)*x**2 + ufloat(2.00, 0.01)*x + ufloat(-4.00, 0.01)

# função raiz(função, valor_inicial)
# apenas execute shit+enter no teclado ou toque em Run

raiz(f, 5)

1.2360679775584056+/-0.004930681752864231

Sitema de equações

Exemplo 6

Calcular o sistema linear formado por :

# definindo a matriz dos coeficientes A e o vetor dos termos independentes b
# apenas execute shit+enter no teclado ou toque em Run

A = unumpy.matrix([[ufloat(1.00, 0.05), ufloat(1.00, 0.05), ufloat(1.00, 0.05)],
                   [ufloat(1.00, 0.05), ufloat(2.00, 0.05), ufloat(2.00, 0.05)], 
                   [ufloat(2.00, 0.05), ufloat(1.00, 0.05), ufloat(3.00, 0.05)]])

b = unumpy.matrix([[ufloat(6,0.5)], [ufloat(9,0.5)],[ufloat(11,0.5)] ])

# imprimir matriz A
# apenas execute shit+enter no teclado ou toque em Run

A

matrix([[1.0+/-0.05, 1.0+/-0.05, 1.0+/-0.05],
        [1.0+/-0.05, 2.0+/-0.05, 2.0+/-0.05],
        [2.0+/-0.05, 1.0+/-0.05, 3.0+/-0.05]], dtype=object)

# imprimir vetor dos termos independentes b
# apenas execute shit+enter no teclado ou toque em Run

b

matrix([[6.0+/-0.5],
        [9.0+/-0.5],
        [11.0+/-0.5]], dtype=object)

# calcular a solução
# apenas execute shit+enter no teclado ou toque em Run
# o resultado é um vetor com os valores de x, y e z

A.I.dot(b)

matrix([[2.9999999999999982+/-1.1937336386313322],
        [2.0+/-0.46233105022267323],
        [1.0000000000000009+/-0.8852965604812887]], dtype=object)

print(f"{A.I.dot(b)}")

[[2.9999999999999982+/-1.1937336386313322]
 [2.0+/-0.46233105022267323]
 [1.0000000000000009+/-0.8852965604812887]]

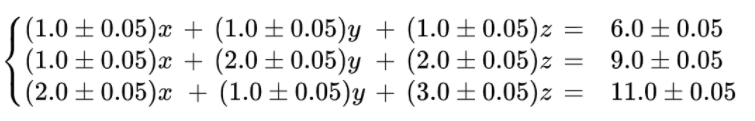
Cálculo diferencial e integral

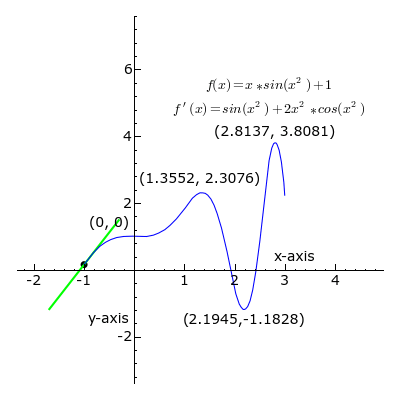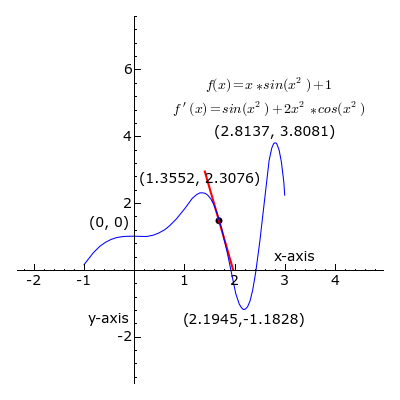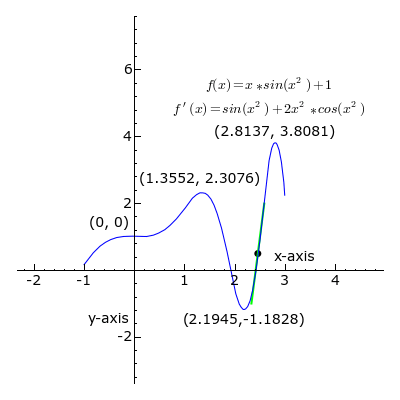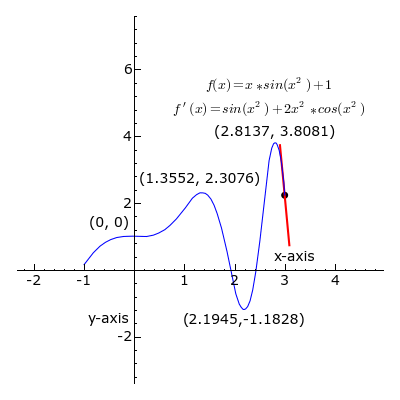
Podemos definir a derivada em um ponto de uma função ${\displaystyle y=f(x)}$ como sendo a taxa de variação instantânea de $y$ em relação a $x$ neste ponto. Geometricamente, a derivada de uma função $f(x)$ em um ponto a fornece o coeficiente angular da reta tangente ao gráfico desta função no ponto $(a, f(a))$.

$\displaystyle \frac{d}{dx}f(a) = f'(a)=\lim _{{x\rightarrow a}}{\frac {f(x)-f(a)}{x-a}}$

A definição de integral de uma função ${\displaystyle {f(x)}}$ no intervalo fechado $[a,b]$ é igual ao limite do somatório de cada um dos valores da função $f(x)$ entre de 0 e n, multiplicados por ${\displaystyle \Delta x.}$

${\displaystyle {\int _{a}^{b}}{f(x)}dx=\lim _{\Delta x\to 0}\sum _{i=0}^{n}{f(x_{i})}\Delta x}$

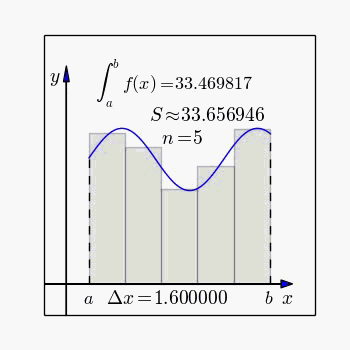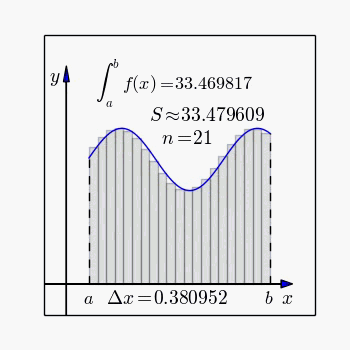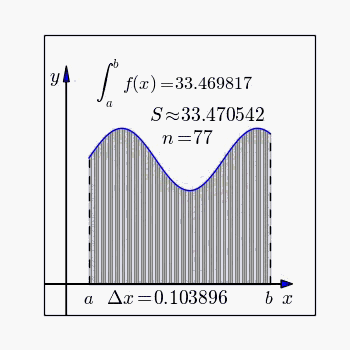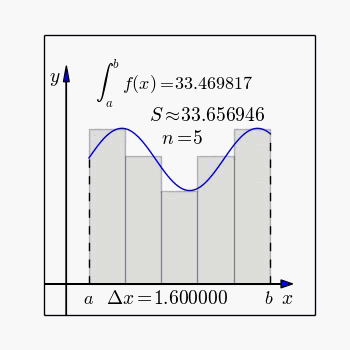
Integral indefinida:

$~~~~~~~~~~\displaystyle \int f(x)~dx$

Integral definida:

$~~~~~~~~~~\displaystyle \int_{0}^{5} f(x)~dx$

Tabela de derivadas e integrais

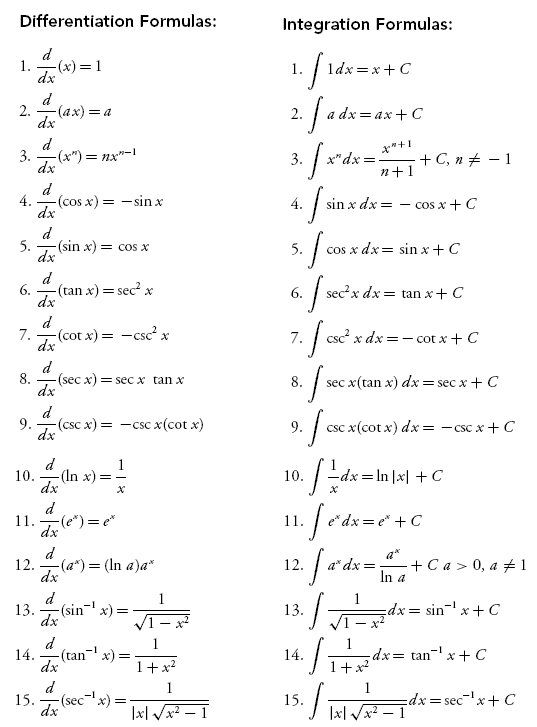
Exemplo 7

Dada a função $\displaystyle f(x) = ax^2 + bx + c$ sendo $a = 3.00 \pm 0.05, ~b = 2.00 \pm 0.05, ~c = 1.00 \pm 0.05$, calcular a derivada no ponto $x = 6,00$ e a integral entre $x_1 = 0,00, ~ x_2 = 6,00$. Gráfico:

# carregar pacotes
# baixe o arquivo FexIFC (https://cocalc.com/share/public_paths/efa6e5fb3c94df8894a02431c032a463179e94dc/Elementos-Python-Julia-Fisica-experimental%2FFexIFC.py)
# coloque na mesma pasta do arquio ipynb que está executando

from FexIFC import *

# definir a função
# apenas execute shit+enter no teclado ou toque em Run

def f(x):
    return ufloat(3.00, 0.05)*x**2 + ufloat(2.00, 0.05)*x + ufloat(1.00, 0.05)

# derivada definida de uma função em x = 6
# apenas execute shit+enter no teclado ou toque em Run

derivada(f, 6)

38.0+/-1.4

# integral definida de x = 0 a x = 6b
# apenas execute shit+enter no teclado ou toque em Run

integral(f, 0, 6)

258.00+/-0.12

# treino
# calcular a derivada de f(x) = e^x + 2 no ponto x_1 = 0.0

# treino
# integral definida de x=0 a x=6

Importar arquivos de dados

Instalar pacote Pandas. Se ja instalou não precisa instalar novamente. Para processar o cálculo execute shit+enter no teclado ou toque em Run

# importar pacotes
# apenas execute shit+enter no teclado ou toque em Run

from FexIFC import *
from pandas import *
from statistics import *
from matplotlib.pyplot import *

Exemplo 8

Importar dos dados da aceleração g de Luzerna a partir de um arquivo CSV.

# importar dados de um arquivo CSV
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

dados = read_csv('Arquivos/aceleracao-g-luzerna.csv')
dados

# calcular a quantidade de dados da aceleração
# Para processar o cálculo execute shit+enter no teclado ou toque em Run

n = len(dados.Aceleracao_g)
n

100

Cálculo da incerteza de dados repetidos

slides de referência

Histograma

O histograma é uma representação gráfica de uma distribuição de frequência de dados por meio de retângulos. Para dados experimentais repetidos de uma grandeza física, o histograma tende, conforme o número de medições, a uma curva normal. Para abaixo de 100 pontos de dados, é necessário ajustar a curva através da distribuição $t-student$.

# histograma dos dados da aceleração
# Para processar o cálculo execute shit+enter no teclado ou toque em Run
# o ponto e vírgula oculta o processamento do cálculo
# observe que o histograma é quase uma curva normal

hist(dados.Aceleracao_g);

Média

A Média Aritmética de um conjunto de dados experimentais, é uma medida de tendência central, obtida somando todos os valores e dividindo o valor pelo número de dados desse conjunto. Indica o valor provável da medida.

# média

md = dados.Aceleracao_g.mean()
md

9.735746278690002

Desvio Padrão

O desvio padrão é uma medida de dispersão de um conjunto de dados em torno de uma média. Quanto mais próximo de zero, melhor o dado do desvio padrão, ou seja, indica que os dados coletados do experimento estão mais uniforme possível.

${\displaystyle s={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}}$

# desvio padrão

dP = dados.Aceleracao_g.std()
dP

0.014329568009809418

Desvio da Média

$\displaystyle s_m = \frac{\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}{\sqrt{n}} = \frac{s}{\sqrt{n}}$

# desvio padrao da média (incerteza padrão)

dPm = dP/sqrt(n)
dPm

0.0014329568009809417

Os dados de um experimento repetido tendem a formar uma curva no formato de "sino", conhecida como curva normal. Para ajustar os dados à uma curva normal, é necessário multiplicar a incerteza padrão por um número que corresponde ao coeficiente de student, que depende do número de dados e precisão da incerteza.

# incerteza padrão ajustada

t = 

# treino: 
# importar os dados da aceleração g em Macapá

# treino
# plotar o histograma

# treino
# calcular a média dos dados da aceleração g em Macapá 

# treino
# calcular o desvio padrão dos dados da aceleração g em Macapá 

# treino
# calcular o desvio padrão médio dos dados da aceleração g em Macapá 

# treino
# calcular a incerteza padrão ajustada dos dados da aceleração g em Macapá 

Parte II

Interpolação

Chapra e Canale (2008) definem a interpolação como a estimativa de valores entre pontos discretos bem conhecidos. A interpolação serve para determinar a correspondência $x_{interp}$ -> y_{interp} entre dois pontos A(x1, y1) e B(x2, y2) conhecidos. Os resultados de medições experimentais fornecem, em geral, um conjunto de valores em pontos discreto. O processo de calcular os valores intermediários aos valores conhecidos é chamado interpolação. Os polinômios interpoladores de Lagrange formam uma classe específica de polinômios que podem ser usados para fazer o ajuste de um determinado conjunto de dados simplesmente a partir dos valores dos pontos (GILAT, 2008).

# dados iniciais tempo em segundo e posição em metros.

tempo   =[ufloat(0.00,0.01), ufloat(1.00,0.01), ufloat(2.00,0.01), ufloat(3.00,0.01), ufloat(4.00,0.01)]
posicao =[ufloat(0.00,0.05), ufloat(1.00,0.05), ufloat(4.00,0.05), ufloat(9.00,0.05), ufloat(16.00,0.05)];

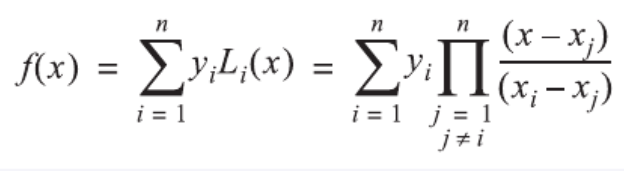
Exemplo 9

De acordo com o gráfico abaixo temos a variação das posições de um carro em função do tempo. Calcular a posição quando t = 3.5s

# carrear pacotes
from FexIFC import *

# calcular posição para tempo = 3.5s

interpolacao(3.5, tempo, posicao)

12.25+/-0.09660010139665358

# treino
# encontrar a função interpolação para os dados tempo = [0,1,2,3,4,5] e posicao = [15,20,28,45,70,150]
# faça o gráfico no scidavis para visualizar melhor os dados

# treino
# calcular a posição para tempo = 4.7s

Referências Bibliográficas

CHAPRA, Steven C.; Canale. Raymond P. Métodos Numéricos para Engenharia, 5ª ed, McGraw Hill, 2008, ISBN: 978-85-86804-87-8.

GILAT, A.; Subramaniam, V. Métodos Numéricos para Engenheiros e Cientistas: Uma Introdução com Aplicações Usando o MATLAB. 1. ed. Bookman, 2008.

PIACENTINI, J.J. Introdução ao Laboratório de Física. Editora da UFSC, 2012.