Book a Demo!
CoCalc Logo Icon
StoreFeaturesDocsShareSupportNewsAboutPoliciesSign UpSign In
Download

The Geometry of Markov Chains

70 views
Tweet
Share
Share

The fuction that does the transformations is hidden in the next cell. If you want to play around at the bottom of this ws just run the cell first. Feel free to copy the code for your own purposes.

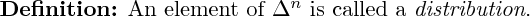
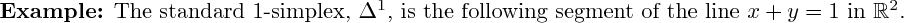
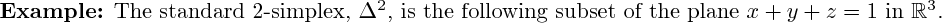
3D rendering not yet implemented
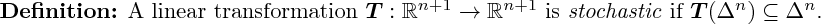
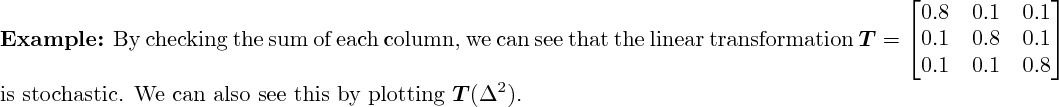
3D rendering not yet implemented
3D rendering not yet implemented
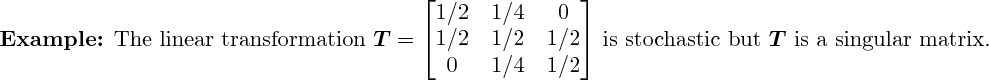
3D rendering not yet implemented
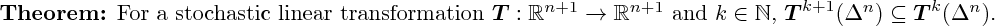
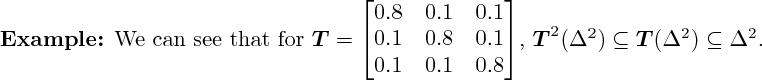
3D rendering not yet implemented
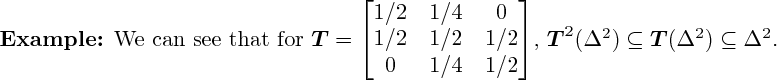
3D rendering not yet implemented
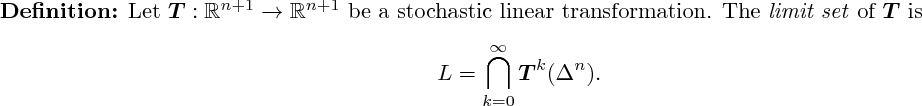
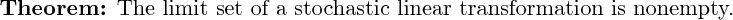
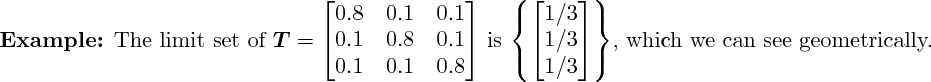
3D rendering not yet implemented
T = matrix([[1/2,1/2,0],[1/4,1/2,1/4],[0,1/2,1/2]])
polygon3d([(1,0,0),(0,1,0),(0,0,1)], opacity=0.3) + sum([line3d([(T^k)[0]+k*vector([0.0001,0.0001,0.0001]),(T^k)[2]+k*vector([0.0001,0.0001,0.0001])], thickness = 2*k, color = Colors[mod(k-1,len(Colors))]) for k in [1..6]])
3D rendering not yet implemented
(1011012001011120111111910)\displaystyle \left(\begin{array}{rrr} \frac{10}{11} & 0 & \frac{1}{20} \\ 0 & \frac{10}{11} & \frac{1}{20} \\ \frac{1}{11} & \frac{1}{11} & \frac{9}{10} \end{array}\right)
3D rendering not yet implemented
(91011012011091012000910)\displaystyle \left(\begin{array}{rrr} \frac{9}{10} & \frac{1}{10} & \frac{1}{20} \\ \frac{1}{10} & \frac{9}{10} & \frac{1}{20} \\ 0 & 0 & \frac{9}{10} \end{array}\right)
3D rendering not yet implemented
(91011001109100001)\displaystyle \left(\begin{array}{rrr} \frac{9}{10} & \frac{1}{10} & 0 \\ \frac{1}{10} & \frac{9}{10} & 0 \\ 0 & 0 & 1 \end{array}\right)
3D rendering not yet implemented
(180780781878180)\displaystyle \left(\begin{array}{rrr} \frac{1}{8} & 0 & \frac{7}{8} \\ 0 & \frac{7}{8} & \frac{1}{8} \\ \frac{7}{8} & \frac{1}{8} & 0 \end{array}\right)
3D rendering not yet implemented
(780181878001878)\displaystyle \left(\begin{array}{rrr} \frac{7}{8} & 0 & \frac{1}{8} \\ \frac{1}{8} & \frac{7}{8} & 0 \\ 0 & \frac{1}{8} & \frac{7}{8} \end{array}\right)
3D rendering not yet implemented
(187800187878018)\displaystyle \left(\begin{array}{rrr} \frac{1}{8} & \frac{7}{8} & 0 \\ 0 & \frac{1}{8} & \frac{7}{8} \\ \frac{7}{8} & 0 & \frac{1}{8} \end{array}\right)
3D rendering not yet implemented
(780180187818780)\displaystyle \left(\begin{array}{rrr} \frac{7}{8} & 0 & \frac{1}{8} \\ 0 & \frac{1}{8} & \frac{7}{8} \\ \frac{1}{8} & \frac{7}{8} & 0 \end{array}\right)
3D rendering not yet implemented
(180787818007818)\displaystyle \left(\begin{array}{rrr} \frac{1}{8} & 0 & \frac{7}{8} \\ \frac{7}{8} & \frac{1}{8} & 0 \\ 0 & \frac{7}{8} & \frac{1}{8} \end{array}\right)
3D rendering not yet implemented
(120120121212120)\displaystyle \left(\begin{array}{rrr} \frac{1}{2} & 0 & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & 0 \end{array}\right)
3D rendering not yet implemented
(10116011160078)\displaystyle \left(\begin{array}{rrr} 1 & 0 & \frac{1}{16} \\ 0 & 1 & \frac{1}{16} \\ 0 & 0 & \frac{7}{8} \end{array}\right)
3D rendering not yet implemented
T = matrix([[1,0,0],[1/8,7/8,0],[1/8,0,7/8]])
show(T.transpose())
repeated_transform(T,25)
(1181807800078)\displaystyle \left(\begin{array}{rrr} 1 & \frac{1}{8} & \frac{1}{8} \\ 0 & \frac{7}{8} & 0 \\ 0 & 0 & \frac{7}{8} \end{array}\right)
3D rendering not yet implemented
T = matrix([[1,0,0],[0,7/8,1/8],[1/8,0,7/8]])
show(T.transpose())
repeated_transform(T,20)
(1018078001878)\displaystyle \left(\begin{array}{rrr} 1 & 0 & \frac{1}{8} \\ 0 & \frac{7}{8} & 0 \\ 0 & \frac{1}{8} & \frac{7}{8} \end{array}\right)
3D rendering not yet implemented
T = matrix([[7/8,0,1/8],[0,7/8,1/8],[1/8,0,7/8]])
show(T.transpose())
repeated_transform(T,20)
(780180780181878)\displaystyle \left(\begin{array}{rrr} \frac{7}{8} & 0 & \frac{1}{8} \\ 0 & \frac{7}{8} & 0 \\ \frac{1}{8} & \frac{1}{8} & \frac{7}{8} \end{array}\right)
3D rendering not yet implemented
T = matrix([[1,0,0],[0,9/10,-1/10],[0,1/10,9/10]])
show(T.transpose())
repeated_transform(T,50)
(10009101100−110910)\displaystyle \left(\begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{9}{10} & \frac{1}{10} \\ 0 & -\frac{1}{10} & \frac{9}{10} \end{array}\right)
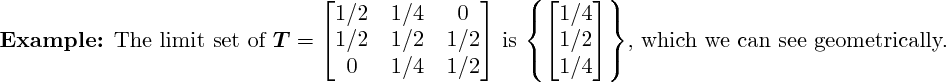
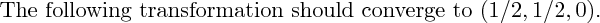
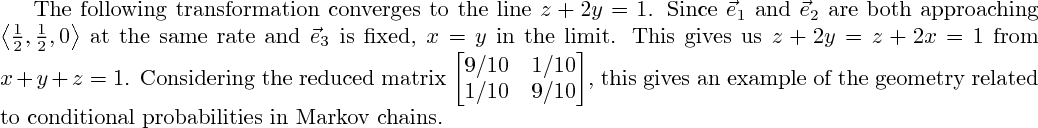
3D rendering not yet implemented