Palestra de divulgação de matemática
O número perdido e o número escondido
Pedro PatrícioDepartamento de Matemática e Aplicações - Universidade do Minho[email protected]http://w3.math.uminho.pt/~pedro/npne/npne.html
Oppps... a mensagem chegou errada!
Uma mesnsagem pode conter err0z e m3smo assim ser intendida.
O contexto ou a palavra podem induzir o que se quereria escrever.
Podemos até poupar simb!
ISBN
10 símbolos
0+1 Língua inglesa
2 Língua francesa
3 Língua alemã
.
.
.
.
.
.
85 Brasil
.
.
.
.
.
.
972 + 989 Portugal
9 7 2 – 6 6 2 – 7 9 2 – 3
x10 x9 x8 x7 x6 x5 x4 x3 x2 x1
, múltiplo de 11.
972-987-655-?
Portanto, tem que ser um múltiplo de 11.
O múltiplo de 11 mais próximo (e maior) que 364 é 374.
Logo, .
Tomamos
European Article Number; EAN-13
O EAN é um código de barras para identificação de produtos.

Está dividido em 4 partes:
- identificação da origem
- identificação da empresa
- identificação do produto
- dígito de controlo


560−1493−11550−6
Algoritmo the Luhn
5∗2,1∗2,3∗2,5∗2,7∗2,9∗2,1∗2,3∗2
1,2,6,1,5,9,2,6
1+4+2+2+6+4+1+6+5+8+9+0+2+2+6+4
Cartão de Cidadão

segue o algoritmo ISBN
indica a versão. , , etc.
, , ..., .
Número de Identificação na Segurança Social - NISS
11 algarismos, sendo o último o de controlo. NISS de Pessoa Singular começa por 1. NISS de Pessoa Colectiva começa por 2.
Por exemplo, .

Brincando aos espiões (ou a arte de esconder mensagens)
A necessidade de transmissão de informação entre dois agentes, de forma a que um terceiro não possa compreender a mensagem, leva a que, de alguma forma, esta esteja ou dissimulada ou cifrada. O primeiro método é denominado por esteganografia, e foi usado por várias civilizações antigas. Por exemplo, uma mensagem poderia ser tatuada numa cabeça rapada de um escravo, ficando escondida assim que o cabelo crescesse, é um exemplo de esteganografia usada pelos gregos antes da nossa era. Outros exemplos incluem o uso de tinta invisível, ou na era actual a inserção de ruído em fotografias digitais.

Nesta figura, está escondida a seguinte:

|
Figura: Apenas mantendo os últimos 2 bits da componente de cor, e aumentado o brilho. (fonte: wikipedia) |
Corre o rumor que a al-Qaeda fez uso da esteganografia para comunicar com os seus membros, nomeadamente no planeamento dos ataques do 11 de Setembro.
No segundo método é aplicado, de alguma forma, um algoritmo que transforme a mensagem numa outra de tal maneira que uma terceira pessoa não a consiga interpretar. De uma forma mais ampla, a criptologia (do gregos cryptos+logos, ou esconder+ciência) divide-se em dois ramos: a criptografia, que estuda a forma de cifrar textos de forma eficiente, e a criptanálise que tenta, por seu turno, quebrar as cifras.
Um sistema criptográfico é um 5-uplo onde conjuntos finitos de símbolos
- conjunto finito de chaves
- conjuntos de funções de cifração/decifração, onde com .
Ou seja, se decifrarmos e que foi cifrado, obtemos a mensagem original.
Por exemplo, considere-se
, letra que sucede a . Aplicando a função de cifração a cada letra da palavra que queremos ``esconder'',
Como é óbvio, a (única) função de decifração para esta chave está definida por letra que antecede a .
A cifra por substituição
Neste caso, consideramos . O conjunto das chaves é constituído por \textbf{todas} as trocas possíveis (permutações) de letras do alfabeto.
Como o número de chaves cresce de forma desmesurada em relação ao número de caracteres do alfabeto, a busca, por uma terceira pessoa, de uma função de decifração por ``força bruta'' é inviável. No entando, existem outras formas de quebrar esta cifra, fazendo uso da análise frequencista do texto cifrado. Como exemplo, considere-se a seguinte permutação :
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| X | N | Y | A | H | P | O | G | Z | Q | W | B | T |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| S | F | L | R | C | V | M | U | E | K | J | D | I |
Para cifrar ``zacarias'' basta-nos procurar a correspondência de cada letra na tabela apresentada. O resultado final é ``IXYXCZXV''.
Uma técnica criptanalítica aplicável é a do estudo frequencista das letras. Por exemplo, em ``IXYXCZXV'' a letra ``X'' surge 3 vezes, pelo que ``X'' deve ser a correspondência das letras mais usadas em português. Torna-se, portanto, essencial a existência de uma tabela com as frequências das letras. Essa tabela existe: a tabela de Beker e Piper.
O gráfico seguinte apresenta a frequência relativa das letras em português. Provavelmente ``X'' é a letra ``a'' cifrada.

Além do estudo de frequência de letras isoladas, poder-se-ia também estudar os digramas e trigramas. Por exemplo, o digrama ``qu'' surge com mais frequência (seguramente!) que o digrama ``hn'', e a letra ``q'' surge mais vezes sucedida de ``u'' do que de outra letra. Os trigramas ``sim'' e ``nao'' são garantidamente mais frequentes que ``dsa'' e ``pot''. Estes exemplos mostram como um criptanalista pode quebrar uma cifra que tem um número demasiado alto de chaves fazendo uso da análise frequencista.
O filósofo árabe do século VIII, Abu'Abd Al-Rahman al-Khalil ibn Ahmad ibn'Amr ibn Tammam al Farahidi al Zadi al Yahmadi cuja obra Kitab al-muamma - O livro da linguagem secreta - foi inspirada pela decifração que Al-Khali l fez de um criptograma grego que o imperador bizantino lhe tinha enviado. Nessa decifração ele utilizou um método criptanalítico que se baseava na suposição do início do texto original ser ``Em nome de Deus'' ou algo semelhante (era comum na época iniciarem-se as mensagens dessa forma), demorando um mês para solucionar o problema.

Mais tarde, este método tornou-se padrão e chegou a ser utilizado na Segunda Guerra Mundial para decifrar mensagens da máquina Enigma (a que faremos referência mais adiante). A descrição mais antiga de análise de frequências explorada para quebrar cifras deve-se a Abu Yusuf Ya'qub ibn Is-haq ibn as-Sabba h ibn 'omran ibn Ismail Al-Kindi, referenciada no seu tratado, redescoberto em 1987, intitulado Risalah fi Istikhraj al Mu'amma - Um Manuscrito sobre a Decifração de Mensagens Criptográficas.
Apesar dos gregos terem escrito vários trabalhos teóricos realacionados com cifras de transposição (as letras da mensagem são reordenadas segundo um certo algoritmo) e de de substituição (as letras mantêm as sua posição mas perdem a sua identidade segundo um certo algoritmo), não se conhecem referências que as tivessem aplicado para fins militares. A primeira alusão à utilização de cifras com esses fins deve-se aos romanos - a Cifra de César. Foi esta a primeira cifra de substituição documentada, utilizada para fins militares, que surgiu na obra De Bello Gallico (Guerras Gálicas), de Júlio César (101 a.C. - 44 a.C.).
Para melhor explicarmos o funcionamento desta (e de outras) cifra, façamos uma curta referência à aritmética modular.
Em primeiro lugar, considere-se o conjunto identificado com , onde definimos as operação de soma e multiplicação como as operações usuais, após as quais tomamos o resto da divisão inteira por 26. Por exemplo,
Como exemplo,
Cifra shift
Nesta cifra, a chave é um elemento de , conhecido pelo emissor e pelo receptor.
O símbolo indica se que tomou o resto da divisão por 26 (para sermos mais correctos, dever-se-ia dizer que indica qualquer número que tenha o mesmo resto na divisão inteira por 26, mas preferimos cometer esta incorrecção a forçar a apresentação de mais noções modulares).
Para obtemos a cifra de César. Ou seja, a cada letra da mensagem fazemos corresponder, no alfabeto, aquela que está 3 posições depois.
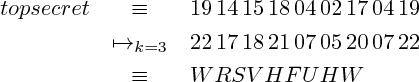
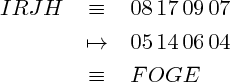
Cifra afim
Nesta cifra, a função de cifração é dada por
A chave, neste caso, é o par .
Claro que quando obtemos cifra Shift. Para a implementação desta cifra, precisamos de ter algumas cautelas. Vejamos o seguinte exemplo:
.
.
Ou seja ``f'' e ``h'' são cifrados no mesmo caracter: o ``U''.
Para que a função de cifração seja injectiva (e, portanto, bijectiva), é necessário e suficiente que
Este facto permite garantir a existência de um certo elemento tal que .
O conjunto das chaves é , e são em número .
As função de cifração e decifração são, respectivamente,
Por exemplo,
Cifra de Vigenère
Nas cifras descritas atrás, uma vez escolhida a chave de cifração cada letra do alfabeto é aplicada numa outra única letra do alfabeto. Daí chamarem-se monoalfabéticas. Apresentamos, de seguida, uma cifra que não é monoalfabética: por exemplo, a letra ``a'' não é garantidamente aplicada numa mesma letra.
Esta cifra foi criada por Blaise Vigenère (1523-1596), usando as ideias de Leon Battista Alberti (1404-1472), Johannes Trithemius (1462-1516) e Giambattista Della Porta (1535-1615). Deve-se, aliás, a Alberti a idealização da primeira cifra polialfabética. Alberti propunha a utilização de dois ou mais alfabetos de cifra e a alternância entre eles durante a cifragem, com o objectivo de confundir os potenciais criptanalistas. Não conseguiu, contudo, transformar a sua ideia num sistema de cifra plenamente elaborado.
Façamos a descrição da cifra de Vigenère. A mensagem é cifrada por blocos e não letra a letra. Suponha que cada bloco tem comprimento . Dada uma chave ,
Como exemplo, suponha que a chave é "BLAISE", i.e., , e portanto . repare que o número total de chaves possíveis de comprimento 6 é (ou seja, mais de 300 milhões de chaves)
Para comunicações militares e governamentais, onde a segurança era fundamental, a cifra monoalfabética simples era obviamente inadequada e existia alguma relutância em adoptar a cifra polialfabética, dada a sua complexidade de implementação. Por conseguinte, os criptógrafos da época sentiram necessidade de criar uma cifra intermédia. Um exemplo marcante de uma cifra monoalfabética melhorada, bastante segura, foi a denominada Grande Cifra de Luís XIV(1638-1715), elaborada por Antoine e Bonaventure Rossignol. Após a morte dos seus criadores, ela caiu em desuso e os seus pormenores exactos perderam-se rapidamente. A Grande Cifra de Luís XIV era tão forte que só no século XIX foi decifrada pelo comandante do exértico francês Etienne Bazeries.
Entretanto, a cifra polialfabética de Vigenére continuava a ser, incontestavelmente, a melhor maneira de garantir as comunicações importantes sigilosas. Essa era considerada inquebrável e tornou-se conhecida como "Le Chiffre Indéchiffrable". Porém, por volta de 1854, o matemático Charles Babbage (1791-1871) foi o autor da maior descoberta no domínio da Criptanálise desde o século IX, altura em que os árabes fizeram uso da análise frequencista. Babbage conseguiu quebrar cifras polialfabéticas, e em particular "Le Chiffre Indéchiffrable". Por acasos do destino, acabou por ser o prussiano Friedrich Wilhelm Kasiski (1805-1881) a receber os créditos da quebra da cifra de Vigenère, sendo a técnica por ele desenvolvida conhecida por Teste de Kasiski.
Tempos modernos
Em 1918, o inventor alemão Arthur Scherbius (1878-1929), construiu uma máquina criptográfica baseada em cifradores rotativos - a famosa máquina Enigma.

Esta invenção forneceu ao exército alemão o sistema criptográfico mais seguro do mundo e, por altura da Segunda Guerra Mundial, as comunicações dos alemães estavam protegidas por um nível de cifras sem paralelo.
Ao avanço da criptografia assistiu-se a uma reacção da criptanálise. O British Tabulating Machine Company construiu uma máquina, designada por "Bombe", instalada em Bletchley Park, para determinar as chaves Enigma. Nesta equipa destacou-se Alan Turing (1912-1954) que identificou a maior fraqueza da Enigma e explorou-a.

Para fazer face a uma cifra alemã ainda mais poderosa que a Enigma, a Cifra Lorentz, os aliados, também em Bletchley Park, contruiram um primeiro computador digital programável - o Colossus.

Se no início desta nova era digital a criptografia foi exclusiva dos militares e dos governos, a democratização dos computadores permitiu que as empresas comçassem a investir nesta nova forma de comunicar de uma forma segura. Tal obrigou a que os protocolos fossem standards. N início dos anos setenta, Horst Feistel (1915-1990), ao serviço do Laboratório Thomas J. Watson da IBM, desenvolveu o sistema Lucifer, um algoritmo de cifra candidato a padrão. Este sistema foi submetido a algumas alterações e, em 23 de Novembro de 1976, foi considerado pela NSA - National Security Agency, como padrão e designada por Data Encryption Standard, ou seja, DES.
O problema de troca de chaves continuava em aberto: a única maneira segura de transmitir a chave de uma cifra era enviá-la por mão própria ou, de uma forma menos segura, por correio. Esta problema foi resolvido por Martin Hellman e Whitfield Diffie, e a solução é conhecida por troca de chaves de Diffie-Hellman. Abriram-se, assim, as portas à ciptografia de chaves públicas. O primeiro sistema funcional para este novo tipo de cifra foi proposto em 1977 por Ronald Rivest, Adi Shamir e Leonard Adleman. Esse sistema foi baptizado de RSA.
(Para fazer jus à verdade, o primeiro algoritmo de chave assimétrica (ou de chave pública) foi proposto por James H. Ellis, Clifford Cocks e Malcolm Williamson do Government Communications Headquarters, pertencendo os serviços secretos britânicos, no ínicio da década de 70 do século passado. O seu contributo apenas pôde ser conhecido em 1997.)
O RSA tem, no entanto, um inconveniente: é demasiado lento. Com efeito, o RSA pode ser 100 a 1000 vezes mais lento que o DES. A solução para este problema passa pelo desenvolvimento de esquemas híbridos: é usado um sistema de chave pública (como o RSA) para abrir um canal seguro, e depois de efectuada a troca de chaves é usado um outro de chave privada (como o DES). Um exemplo de software faz uso desta solução é o PGP, ou o ssh.
Actualmente o DES é considerado inseguro (pode ser quebrado em menos de 24 horas), e foi substituído pelo AES.
É importante referir que não são usadas apenas o DES (ou o AES) e o RSA como cifras de chave privada e pública, respectivamente. A cifras RC5, Blowfish, IDEA, NewDES, SAFER, CAST5, FEAL são outros exemplos de chave privada (por exemplo, o PGP usa o IDEA), enquanto que o ElGamal, o ``knapsack'' (que apesar de tomar partido de não se conhecer uma solução ``fácil'' de um certo problema, pode ser quebrada em tempo útil pela forma como está definida), a cifra de McEliece são outros exemplos de cifras assimétricas (ou de chave pública).
RSA com 8 Bits
-
Alice escolhe dois primos p = 11 e q = 7, e calcula
n = p*q = 77.
Calcula ainda
m = (p-1)*(q-1) = 60 e escolhe a = 13 primo relativo com
m = 60.
Calcula b = a-1 mod m = 37.
Publica n = 77 e a = 13 (chave publica de Alice)
-
Bob pretende enviar a mensagem mens = 28 a Alice. Com a chave publica de Alice, calcula
cifrado = mensa mod n = 7.
-
Alice recebe o texto cifrado = 7 de Bob. Usando o inverso b = 37 = a-1 mod m, calcula
decifrado = cifradob mod n = 28.
Questões práticas:
- como encontrar primos?
- onde está a segurança?
- como calcular ?
A divisão trivial...
O teste de Miller-Rabin
RSA: um exemplo "mais real"
Factorização de Fermat
Teorema dos Números Primos
indica o número de primos não superiores a .
Primos GRAAAANDEEEEES
Se é primo então chama-se um primo de Mersènne.
Coisas inúteis...
Conjectura de Goldbach
Todo o número par maior que 4 é soma de dois primos
Conjectura dos primos gémeos
Existe uma infinidade de primos gémeos.
O problema de Siracusa
http://en.wikipedia.org/wiki/Collatz_conjecture
se é par, e se é ímpar.
Conjectura: existe um tal que , independentemente da condição inicial.